Ans.

Let us consider two particles of masses \( m_1 \) and \( m_2 \) having position vectors \( \vec{r_1} \) and \( \vec{r_2} \) respectively with respect to the origin O, have a relative motion between them.

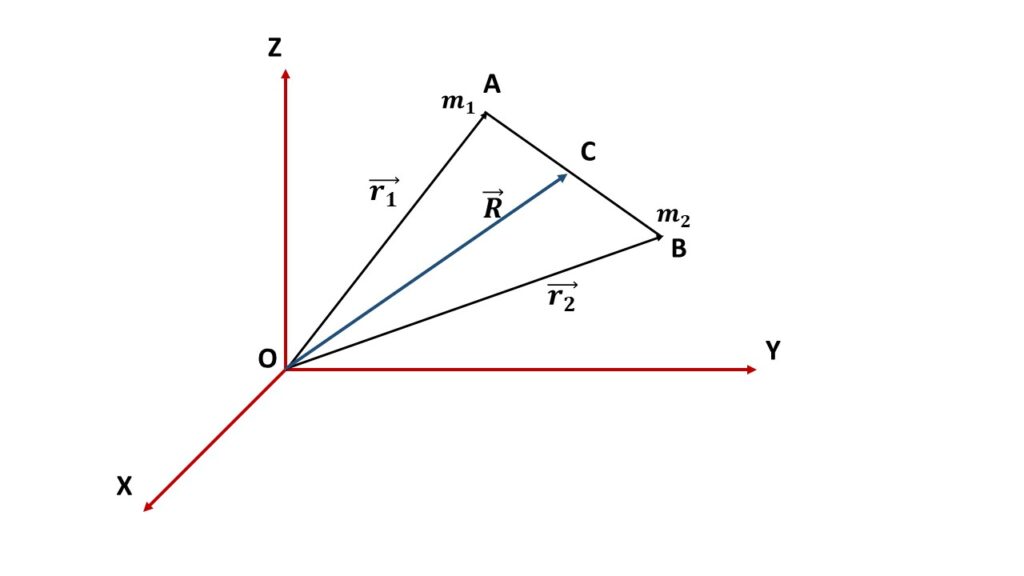
Their centre of mass lies on the line joining them. So the force on \( m_1 \) due to the mass \( m_2 \) and the force on \( m_2 \) due to the mas \( m_1 \) are both directed toward the centre of mass.

let \( f(r)\hat{r} \) be the force on the mass \( m_1 \), so the force on the mass \( m_2 \) will be \( -f(r)\hat{r} \).

Therefore, \( m_1\ddot{\vec{r_1}}=f(r)\hat{r} \) and \( m_2\ddot{\vec{r_2}}=-f(r)\hat{r} \).

so, \( m_1\ddot{\vec{r_1}}+m_2\ddot{\vec{r_2}}=0\tag{1} \)

Let \( \vec{R} \) be the position vector of the centre of mass C with respect to the origin O.

\( \displaystyle{\vec{R}=\frac{m_1\vec{r_1}+m_2\vec{r_2}}{m_1+m_2}} \)

Differentiating both side with respect to time,

\( \dot{\vec{R}}=\frac{m_1\dot{\vec{r_1}}+m_2\dot{\vec{r_2}}}{m_1+m_2} \)

Again differentiating both side with respect to time,

\( \ddot{\vec{R}}=\frac{m_1\ddot{\vec{r_1}}+m_2\ddot{\vec{r_2}}}{m_1+m_2}\tag{2} \)

Using equations (1) and (2) we can write

\( \ddot{\vec{R}}=0 \)

or, \( \dot{\vec{R}}=constant \)

So the centre of mass remains stationary when centre of mass acts between the particles.