Ans.

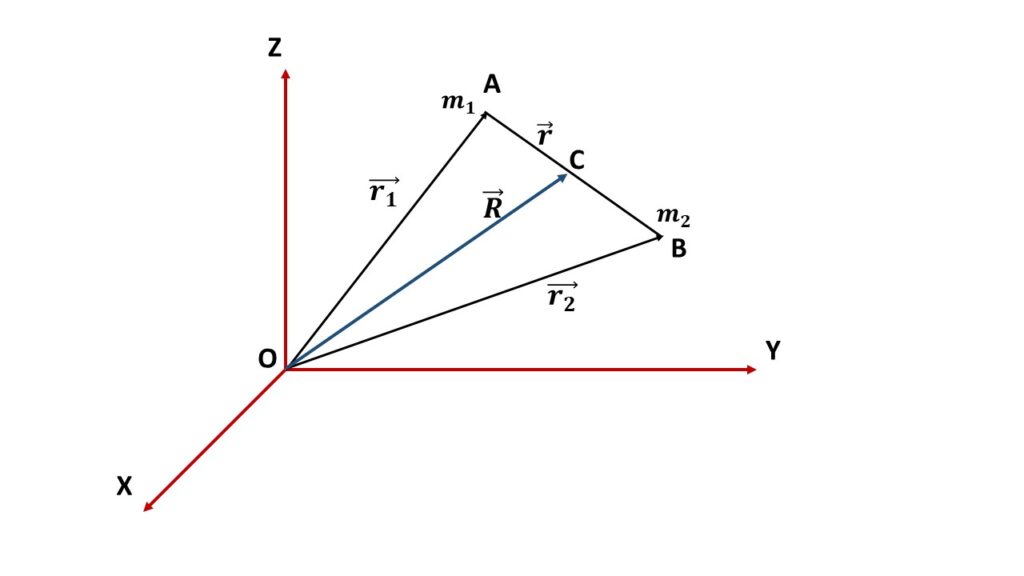
Let us consider a system of two masses \( m_1 \) and \( m_2 \) having position vectors \( \vec{r_1} \) and \( \vec{r_2} \) respectively with respect to the origin O.

If \( \vec{R} \) be the position vector of the centre of mass C of the system with respect to the origin O, then

\( \vec{R}=\frac{m_1\vec{r_1}+m_2\vec{r_2}}{m_1+m_2}\tag{1} \)

Let the two masses \( m_1 \) and \( m_2 \) are separated by a distance \( \vec{r} \) and acted upon by external force \( \vec{F_1} \) and \( \vec{F_2} \) respectively.

Now the internal force on \( m_1 \) due to \( m_2 \) is \( \vec{F_{12}} \),

and the internal force on \( m_2 \) due to \( m_1 \) is equal \( \vec{F_{21}} \).

Since the internal forces on each other satisfy the Newton’s 3rd Law, then

\( \vec{F_{12}}=\vec{F_{21}}\tag{2} \)

Now the equation of motion of the two particles are

\( m_1\ddot{\vec{r_1}}=\vec{F_1}+\vec{F_{12}}\tag{3} \) \( m_2\ddot{\vec{r_2}}=\vec{F_2}+\vec{F_{21}}\tag{4} \)

Multiplying the equations (3) and (4) by \( m_2 \) and \( m_1 \) respectively and subtracting them we get,

\( m_1m_2(\ddot{\vec{r_1}}-\ddot{\vec{r_2}})=(m_2\vec{F_1}-m_1\vec{F_2})+(m_2\vec{F_{12}}-m_1\vec{F_{21}}) \)

or, \( m_1m_2\frac{d^2}{dt^2}(\vec{r_1}-\vec{r_2})=(m_2\vec{F_1}-m_1\vec{F_2})+(m_1+m_2)\vec{F_{12}} \),
[using equation (2)]

or, \( m_1m_2\frac{d^2}{dt^2}(\vec{r_1}-\vec{r_2})= (m_1+m_2)\vec{F_{12}}+m_1m_2(\frac{\vec{F_1}}{m_1}-\frac{\vec{F_2}}{m_2}) \)

or, \( \frac{m_1m_2}{m_1+m_2}\frac{d^2}{dt^2}(\vec{r_1}-\vec{r_2})=\vec{F_{12}}+\frac{m_1m_2}{m_1+m_2}(\frac{\vec{F_1}}{m_1}-\frac{\vec{F_2}}{m_2}) \)

or, \( \mu\frac{d^2\vec{r}}{dt^2}=\vec{F_{12}}+\mu(\frac{\vec{F_1}}{m_1}-\frac{\vec{F_2}}{m_2}) \)

where \( \mu=\frac{m_1m_2}{m_1+m_2} \) is the reduced mass of the system of two particles of masses \( m_1 \) and \( m_2 \). \( \vec{r}=\vec{r_1}-\vec{r_2} \) is the position vector of the of the mass \( m_1 \) with respect to the mass \( m_2 \).

When there is no external force then \( \vec{F_1}+\vec{F_2}=0 \) then

\( \mu\frac{d^2\vec{r}}{dt^2}=\vec{F_{12}} \).

In such case the equation of motion of the two particles system is only due the internal forces arising from the interaction between the two particles.

This equation suggests that a two body problem ay be considered to be equivalent ta one body problem, where one of them is moving and the other is at rest.