Centre of mass:

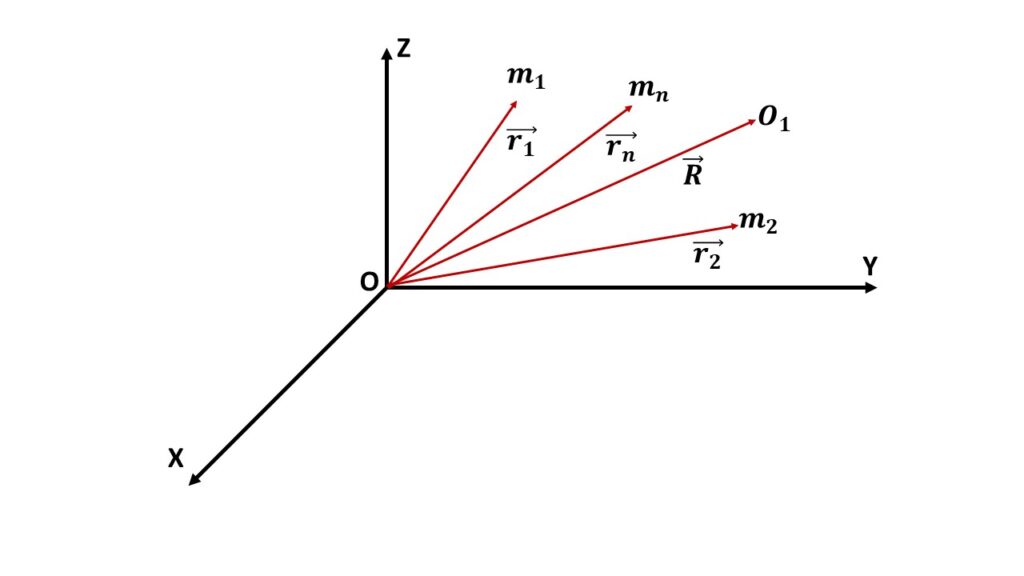
Let us consider a system of n particles of masses m₁, m₂, …. m_n with position vectors \( \vec{r_1} \), \( \vec{r_2} \), \( \cdots \), \( \vec{r_n} \) respectively with respect to the origin O, as shown in the above Fig. 1.

The centre of mass of the system is defined as the point \( O_1 \) with position vector \( \vec{R} \), is given by

\( \vec{R}=\displaystyle{\frac{m_1\vec{r_1}+m_2\vec{r_2}+\cdots+m_n\vec{r_n}}{m_1+m_2+\cdots+m_n}} \)

or, \( \vec{R}=\displaystyle{\frac{\sum_{i=1}^{n}{m_ir_i}}{\sum_{i=1}^{n}{m_i}}} \)

or, \( \vec{R}=\displaystyle{\frac{1}{M}\sum_{i=1}^{n}{m_ir_i}} \)

where, \( \displaystyle{M=\sum_{i=1}^{n}{m_i}} \) is the total mass of the system.

When the centre of mass of the system coincides with the origin O of the system then \( \vec{R}=0 \),

Therefore, \( \displaystyle{\sum_{i=1}^{n}}{m_ir_i} =0\ vector \)

So centre of mass of a system is defined by a point in space, so that the vector sum of the moment of the mass points around it will be zero.

Centre of mass of a system of particles of continuous mass distribution:

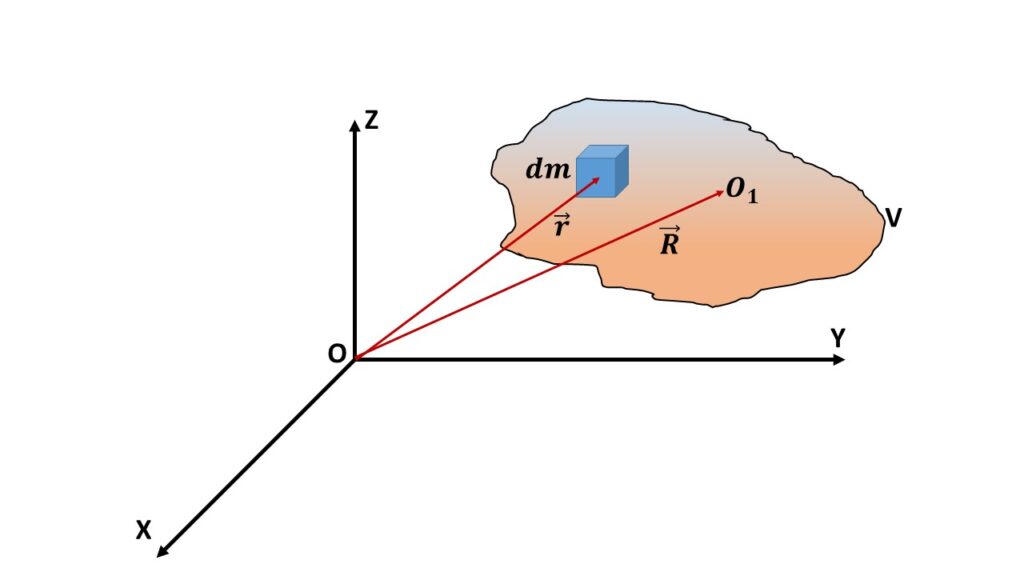
Let us consider a system of particles of continuous mass distribution in a region V as shown in the above Fig. 2. Let us consider s small elementary volume of mass \( dm \) with position vector \( \vec{r} \) with respect to the origin O. If \( \rho \) be the mass density, then the mass of the elementary volume is \( dm=\rho\ dv \), where \( dv \) is the volume of that elementary mass.

So the centre of mass of the system is defined as the point \( O_1 \) having position vector \( \vec{R} \) given by,

\( \vec{R}=\displaystyle{\frac{\int_v\rho\vec{r}dv}{\int_v\rho{dv}}}\\=\frac{1}{M}\displaystyle{\int_v}\rho\vec{r}dv \)

where, \( M=\displaystyle{\int_v}dm=\displaystyle{\int_v}\rho\ dv \) is the total mass of the system.