(i) Moment of inertia of a uniform elliptic lamina or elliptic disc about its minor axis:

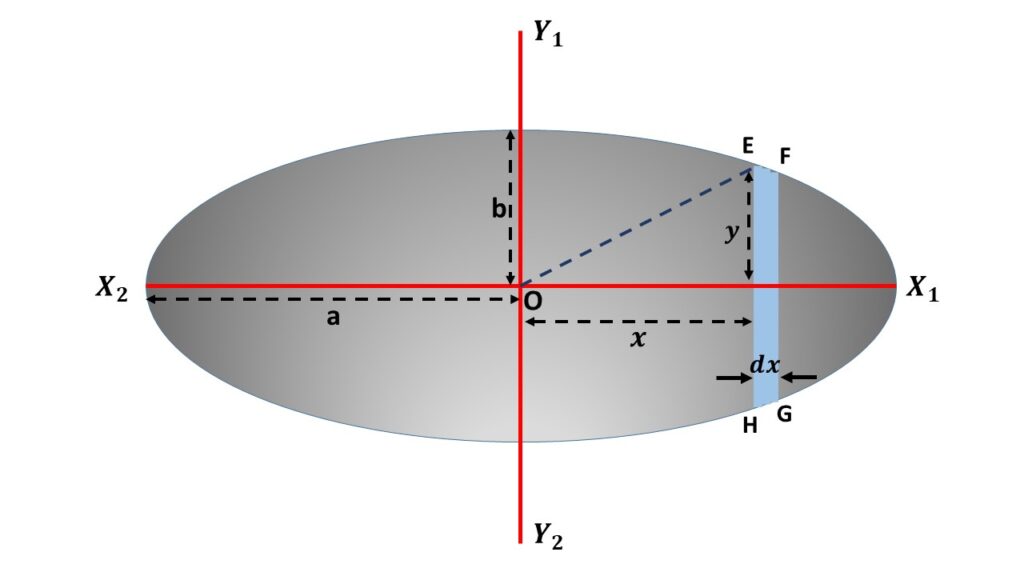
Let us consider a uniform elliptic lamina or elliptic disc of mass M, semi-major axis a and semi-minor axis b. So the total surface area of this elliptic lamina is \( \pi{ab} \) and the mass density i.e., mass per unit surface area is \( \left(\frac{M}{\pi{ab}}\right) \). If the major and the minor axis axes coincide with the co-ordinate axes and the centre of this elliptic disc coincide with the origin of the co-ordinate system then the equation of this ellipse will be,

\( \displaystyle{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1} \)

\( or,\ \displaystyle{y^2=b^2{\left(1-\frac{x^2}{a^2}\right)}} \)

\( or,\ \displaystyle{y=\frac{b}{a}\sqrt{(a^2-x^2)}}\tag{1} \)

In order to calculate the moment of inertia of the elliptic lamina about its minor axis \( Y_1Y_2 \), let us consider an elementary area EFGH at a distance \( x \) from the minor axis \( Y_1Y_2 \) and of thickness \( dx \). So the surface area of this element EFGH is \( 2ydx \) and the mass of this element is \( \left(\frac{M}{\pi{ab}}\right)2ydx \), where \( 2y \) is the length of the element EFGH.

Moment of inertia of this element about the minor axis \( Y_1Y_2 \) is,

\( dI_y=\frac{2M}{\pi{ab}}ydx\times{x^2} \)

\( or,\ dI_y=\frac{2M}{\pi{ab}}\frac{b}{a}\sqrt{(a^2-x^2)}x^2{dx} \)
[putting the value of \( y \) from equation (1) ]

\( or,\ dI_y=\frac{2M}{\pi{a^2}}\sqrt{(a^2-x^2)}x^2{dx} \)

\( or.\ dI_y=f(x)dx \) (say)

So the moment of inertia of the whole elliptic lamina about the axis \( Y_1Y_2 \) is

\( I_y=\displaystyle{\int_{-a}^{a}}dI_y=\displaystyle{\int_{-a}^{a}}f(x)dx \)

since \( f(x) \) is an even functionso we can write,

\( I_y=2\displaystyle{\int_0^a}f(x)dx \)

\( or,\ I_y=2\frac{2M}{\pi{a^2}}\displaystyle{\int_0^a}\sqrt{(a^2-x^2)}x^2{dx} \)

\( or,\ I_y=\frac{4M}{\pi{a^2}}\displaystyle{\int_0^a}\sqrt{(a^2-x^2)}x^2{dx}\tag{2} \)

From Fig. 1 we can write, \( x=a\sin\phi\\or,\ dx=a\cos\phi{d\phi} \)

Putting the value of \( x \) and \( dx \) in equation (2),

\( I_y=\frac{4M}{\pi{a^2}}\displaystyle{\int_0^{\frac{\pi}{2}}}\sqrt{a^2-a^2{\sin}^2\phi}(a^2{\sin}^2\phi){(a\cos\phi){d\phi}} \)

\( or,\ I_y=\frac{4M}{\pi{a^2}}a^4\displaystyle{\int_0^{\frac{\pi}{2}}}({\sin}^2\phi)({\cos}^2\phi){d\phi} \)

\( or,\ I_y=\frac{M}{\pi}a^2\displaystyle{\int_0^{\frac{\pi}{2}}}{\left[2(\sin\phi)(\cos\phi)\right]}^2{d\phi} \)

\( or,\ I_y=\frac{Ma^2}{\pi}\displaystyle{\int_0^{\frac{\pi}{2}}}({\sin}^2{2\phi}){d\phi} \)

\( or,\ I_y=\frac{Ma^2}{\pi}\displaystyle{\int_0^{\frac{\pi}{2}}}\left[\frac{1-\cos{4\phi}}{2}\right]{d\phi} \)

\( or,\ I_y=\frac{Ma^2}{2\pi}{\left[\phi-\frac{\sin{4\phi}}{4}\right]}_0^{\frac{\pi}{2}} \)

\( or.\ \displaystyle{I_y=\frac{Ma^2}{2\pi}\frac{\pi}{2}} \)

\( or,\ \displaystyle{I_y=\frac{Ma^2}{4}}\tag{3} \)

(ii) Moment of inertia of the elliptic lamina about its major axis:

Similarly we can write, when the elliptic lamina or elliptic disc rotates about the major axis \( X_2X_1 \) as shown in Fig. 1, the moment of inertia of the lamina abou the major axis \( X_2X_1 \) is given by,

\( \displaystyle{I_x=\frac{Ma^2}{4}}\tag{4} \)

(iii) Moment of inertia of the elliptic lamina about an axis passing through its centre and perpendicular to the plane of the disc or lamina:

Let us consider the elliptic lamina or elliptic disc of mass M rotates about the axis \( Z_1Z_2 \) passing through the centre O of the disc and perpendicular to the plane of the disc, as shown in the above Fig. 2. So by applying the theorem of perpendicular axes, we can write that the moment of inertia of this lamina about the axis \( Z_1Z_2 \) is

\( I_{Z_1Z_2}=I_x+I_y \)

\( or,\ I_{Z_1Z_2}= \frac{Ma^2}{4}+\frac{Ma^2}{4} \)

\( or,\ \displaystyle{I_{Z_1Z_2}=\frac{1}{2}Ma^2} \)