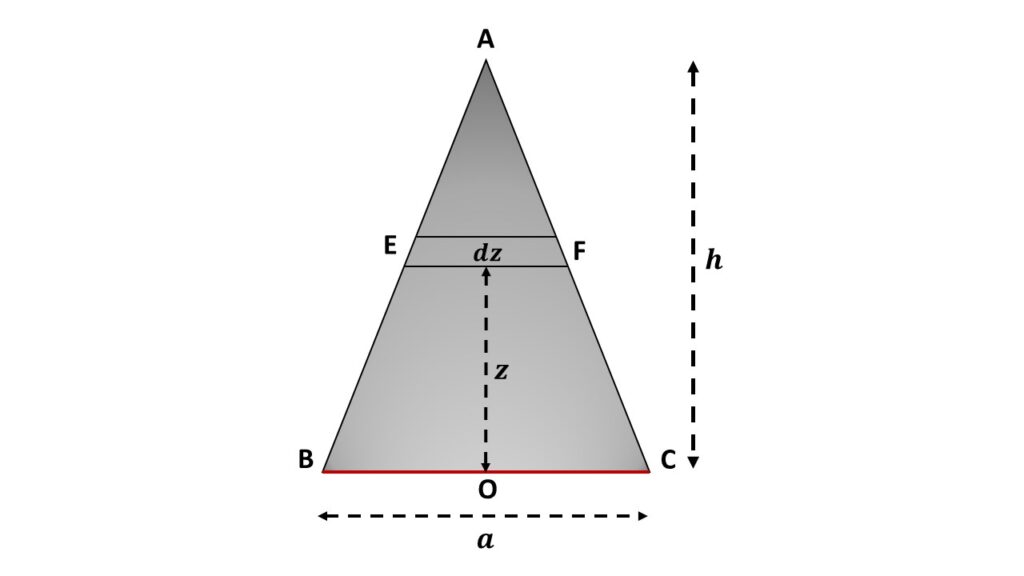
Determine The Moment Of Inertia Of A Triangular Lamina (i) About One Of Its Sides, (ii) About An Axis Passing Through The Centre Of Gravity And Parallel To One Side, (iii) About An Axis Passing Through One Of Its Vertices And Parallel To Opposite Side.

Let us consider a triangular lamina ABC of mass M, is rotating about one of its sides BC, where the length of the side BC is a. If \( h \) be the height of this lamina, then the area of this lamina is \( \left(\frac{1}{2}\cdot{a}\cdot{h}\right) \) and the mass density i.e., mass per unit area is \( \frac{M}{\frac{1}{2}ah} \) = \( \left(\frac{2M}{ah}\right) \).

In order to calculate the moment of inertia of this lamina about the axis of rotation BC, let us consider a small elementary area \( EF \) of thickness \( dz \) and length \( l \) at a distance \( z \) from the axis of rotation BC. So the area of \( EF \) is \( l\cdot{dz} \) and the mass is \( \left(\frac{2M}{ah}\right)l\ dz \). Now the moment of inertia of this element about the axis of rotation is

\( dI=\left(\frac{2Ml}{ah}\right)z^2\ dz\tag{1} \)

From Fig. 1, we can write that

\( \left(\frac{l}{h-z}\right)=\left(\frac{a}{h}\right) \)

\( or,\ \displaystyle{l=\frac{a(h-z)}{h}} \)

Putting the value of \( l \) in equation (1) we get,

\( dI=\left(\frac{2M}{ah}\right)\frac{a(h-z)}{h}z^2\ dz \)

\( or,\ dI=\frac{2M}{h^2}(h-z)z^2\ dz \)

So the moment of inertia of the whole triangular lamina is

\( I=\frac{2M}{h^2}\displaystyle{\int_0^h}(h-z)z^2\ dz \)

\( or,\ I=\frac{2M}{h^2}\displaystyle{\int_0^h}(hz^2-z^3)\ dz \)

\( or,\ I=\frac{2M}{h^2}{\left[\frac{1}{3}hz^3-\frac{1}{4}z^4\right]}_0^h \)

\( or,\ I=\frac{2M}{h^2}{\left[\frac{1}{3}h^4-\frac{1}{4}h^4\right]} \)

\( or,\ I=\frac{2M}{h^2}\frac{1}{12}h^4 \)

\( or,\ \displaystyle{I=\frac{1}{6}Mh^2}\tag{2} \)

(ii) About an axis passing through the centre of gravity and parallel to one side of the triangular lamina:

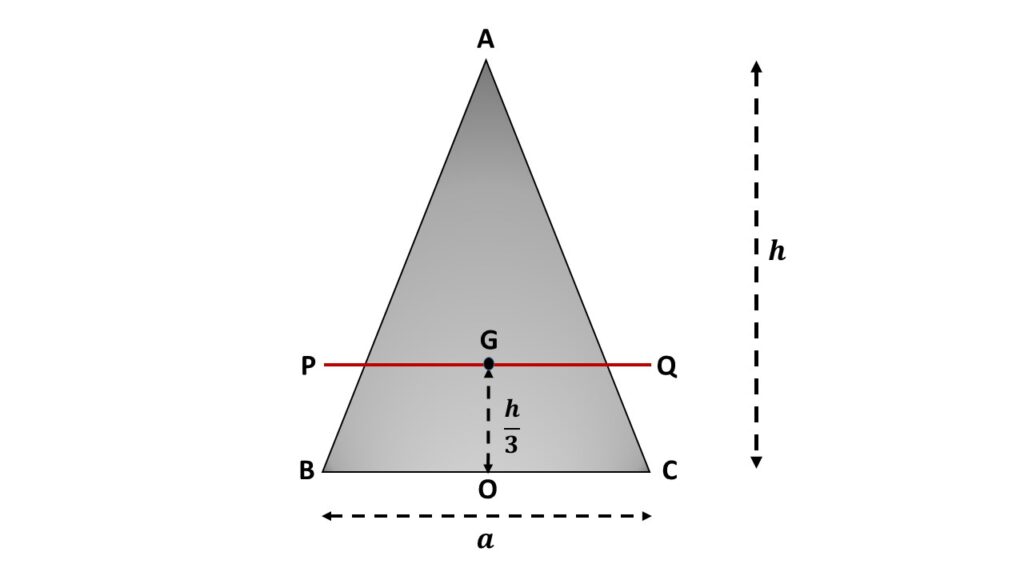
Let us consider the rectangular lamina ABC is rotating about an axis PQ passing through the centre of gravity G of the lamina and parallel to the side BC. We know that the perpendicular distance of G from each side is \( \left(\frac{h}{3}\right) \), where h is the height of the triangular lamina.

So the perpendicular distance between PQ and BC is \( (\frac{h}{3}) \)

If \( I_G \) be the moment of inertia of this lamina about the axis PQ, then by applying the theorem of parallel axes, we can write that

\( I=I_G+M{\left(\frac{h}{3}\right)}^2 \)

\( or,\ I_G=I-\frac{1}{9}Mh^2 \)

\( or,\ I_G=\frac{1}{6}Mh^2-\frac{1}{9}Mh^2 \)
[putting the value of \( I \) from equation (2)]

\( or,\ \displaystyle{I_G=\frac{1}{18}Mh^2}\tag{3} \)

(iii) Moment of inertia of the rectangular lamina about an axis passing through one of its vertices and parallel to opposite side:

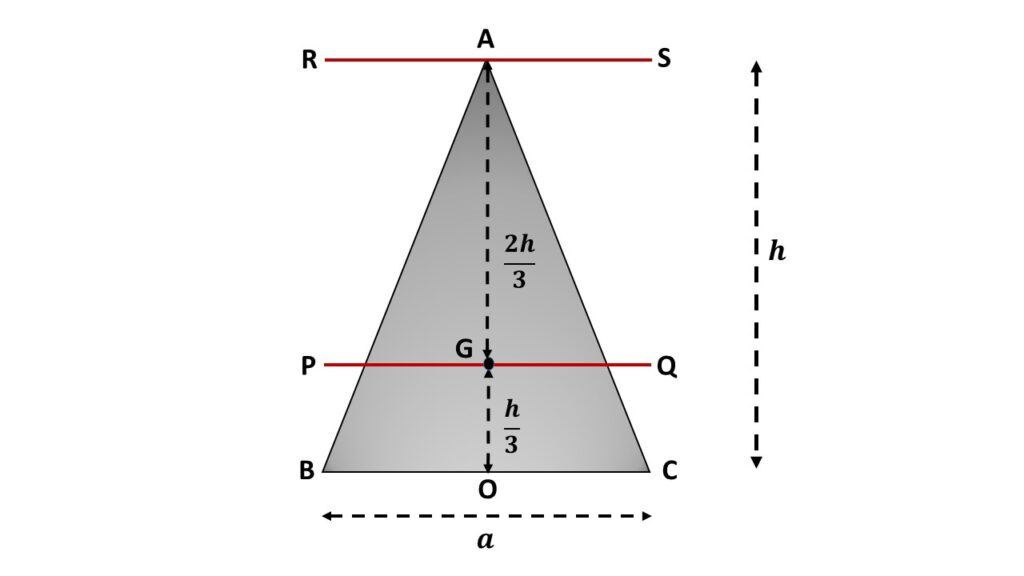
Let us consider the rectangular lamina ABC is rotating about an axis RS passing through vertex A and parallel to the side BC. We know that the distance of each vertex from the centre of gravity is \( \left(\frac{2h}{3}\right) \), where h is the height of the rectangular lamina. So the perpendicular distance between PQ and RS is \( \left(\frac{2h}{3}\right) \).

By applying the theorem of parallel axes, we can write that the moment of inertia of this rectangular lamina about the axis of rotation \( RS \) is

\( I_V=I_G+M{\left(\frac{2h}{3}\right)}^2 \)

\( or,\ I_V=\frac{1}{18}Mh^2+\frac{4}{9}h^2 \)
[putting the value of \( I_G \) from equation (3)]

\( or,\ \displaystyle{I_V=\frac{1}{2}Mh^2}\tag{4} \)