Ans.
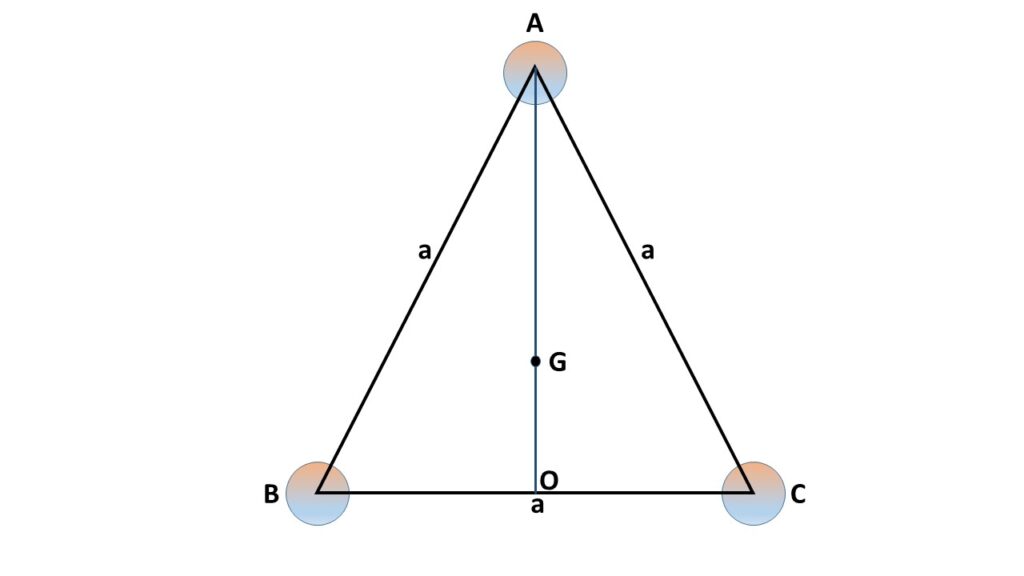
Three spheres of radius ‘r‘ and mass ‘m‘ placed with their centres at the vertices of an equilateral triangle ABC. Here G is the centre of gravity.
From Fig. 1 we can write,
\( AO=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}\\=\frac{\sqrt{3}}{2}a \)
\( AG=\frac{2}{3}AD\\=\frac{2}{3}\times\frac{\sqrt{3}}{2}a\\=\frac{a}{\sqrt{3}} \)
We know that the moment of inertia of a sphere about its diameter \( \frac{2}{5}mr^2 \), [ To know the derivation of moment of inertia of a sphere about its diameter, (CLICK HERE) ].
By applying the theorem of parallel axes, the moment of inertia of each sphere about an axis passing through the centre of gravity G and perpendicular to the plane of the triangle is
\( \frac{2}{5}mr^2+m{\left(\frac{a}{\sqrt{3}}\right)}^2 \)
\( =\frac{2}{5}mr^2+\frac{1}{3}ma^2 \)
\( =m\left(\frac{2}{5}r^2+\frac{1}{3}a^2 \right) \)
So the moment of inertia of the system of three spheres about the axis passing through the centre of gravity G and perpendicular to the plane of the triangle is
\( 3m\left(\frac{2}{5}r^2+\frac{1}{3}a^2 \right) \)
