Motion of an object in the tunnel through the earth from one point to another point of the surface:
Let us consider the earth is a sphere of radius \( R \), mass \( M \), density \( \rho \) and \( O \) is the centre of the earth. \( PQ \) is a straight frictionless tunnel connecting two points \( P \) and \( Q \) on the surface of the earth as shown in the adjoining Fig. 1.
Let \( B \) is the centre of the tunnel \( PQ \) and a perpendicular line \( OB \) is drawn on the point \( B \) from the centre \( O \).
Let, an object of mass \( m \) is moving along the tunnel in the direction \( PQ \), at any instant of time the object is at a point \( A \) at a distance \( x \) from the point \( B \) and at a distance \( r \) from the centre \( O \).
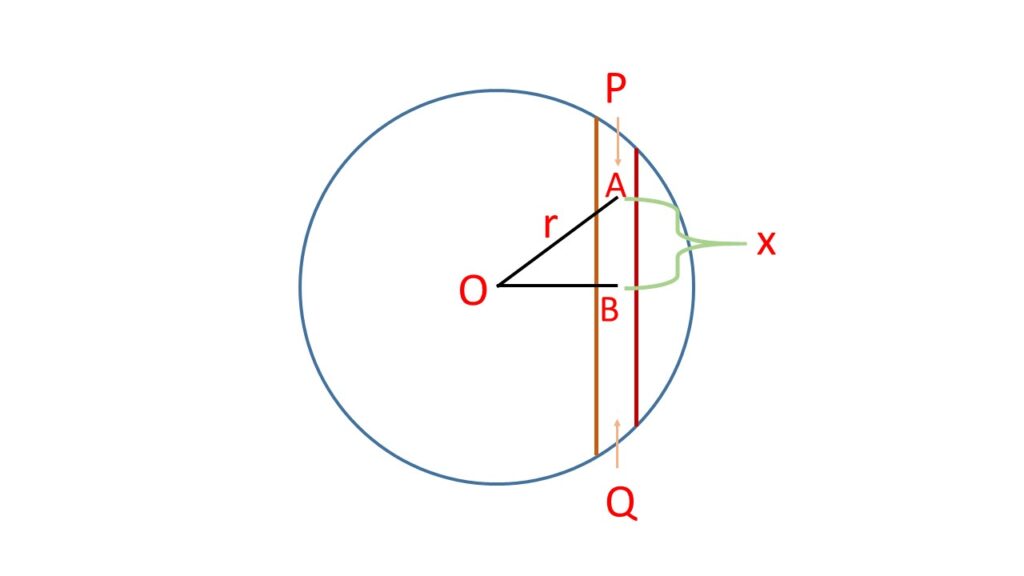
\( OA=r \) and \( AB=x \).
Now the gravitational force of attraction on the mass \( m \) at point \( A \) will be only due to the inner solid sphere of radius \( r \). The shell exterior to it will have no influence on \( m \).
Therefore the gravitational attraction force on \( m \) along \( AO \) is \( F=G\cdot\frac{(\frac{4}{3}\pi{r}^3\rho\cdot{m})}{r^2} \), where \( G \) is the gravitational constant.
or, \( F=G\frac{4}{3}\pi\rho{m}r \)
The component of the force \( F \) along the \( AB \) direction is,
\( F\cos\angle{OAB}= – G\frac{4}{3}\pi\rho{m}r\cdot\frac{x}{r} \\=- G\frac{4}{3}\pi\rho{m}x \)The negative sign indicates that \( F \) and \( x \) are in opposite direction.
So we can write that \( F=-kx \), where \( k=G\frac{4}{3}\pi{m}\rho= constan \).
When an object moves along PBQ, it is acted by a force that is proportional to the distance from the mean position \( B \) and directed towards \( B \). So the motion of the object is a simple harmonic motion.
Time period of oscillation:
We know that the differential equation of such simple harmonic motion is,
\( m\frac{d^2{x}}{{dt}^2}=-kx \\or,\ \frac{d^2{x}}{{dt}^2}+\frac{k}{m}x=0\\ or,\ \frac{d^2{x}}{{dt}^2}+{\omega}^2{x}=0 \)Where, \( \omega=\sqrt{\frac{k}{m}}=\sqrt{G\frac{4}{3}\pi\rho} \)
Now the time period of this simple harmonic motion is, \( T=\frac{2\pi}{\omega}=\frac{2\pi}{ \sqrt{G\frac{4}{3}\pi\rho} }\\ =\sqrt{\frac{3\pi}{G\rho}}\\=\sqrt{\frac{3\pi{4}\pi{R}G}{G3g}} \)
or, \( \displaystyle{T=2\pi\sqrt{\frac{R}{g}}} \)
Where, the acceleration due to gravity on the earth’s surface is,
\( g=\frac{GM}{R^2}=G\frac{\frac{4}{3}\pi{R}^3\rho{M}}{R^2} \\=G\frac{4}{3}\pi{R}\rho \)or, \( \rho=\frac{3g}{4\pi{R}G} \).
Value of time period:
Time period \( T=2\pi\sqrt{\frac{R}{g}}\\=2\pi\sqrt{\frac{6.38\times10^8}{980}}\\=84.4\ minutes\ (approx) \)
where \( R=6.38\times10^6 \) m.
If the tunnel is bored through the centre of the earth, the time period of oscilation will be the same.