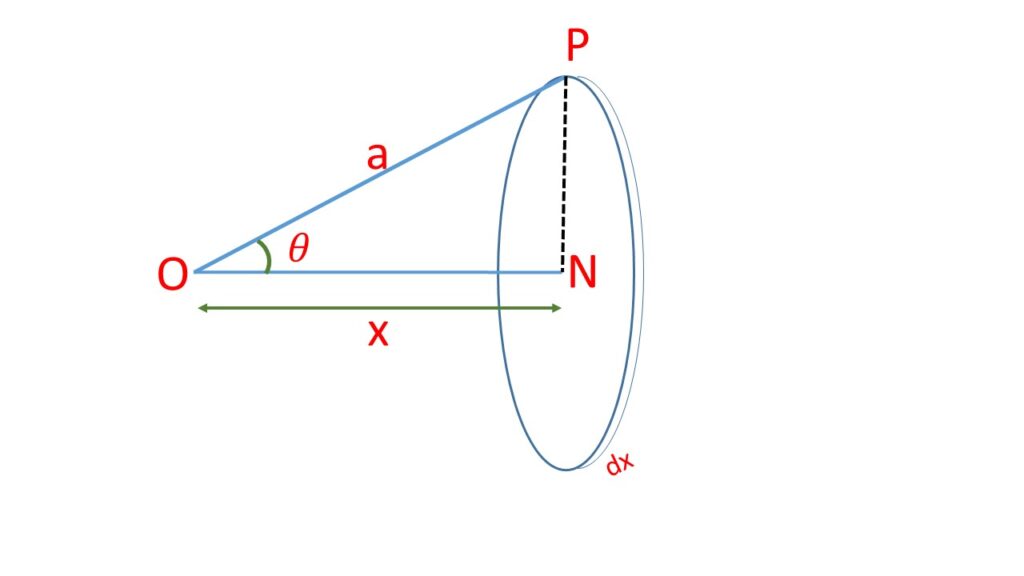
Let us consider a solid sphere of mass “M” and radius “a” and a strip of thickness dx at a distance x from the centre o of the sphere. The radius of the strip is \( PN=a\sin{\theta} \) and the area of the strip is

\( \pi\cdot{(PN)}^2=\pi{a}^2{\sin}^2{\theta} \\=\pi{a}^2(1-{\cos}^2\theta) \\=\pi{a}^2(1-\frac{x^2}{a^2}) \\=\pi(a^2-x^2)\)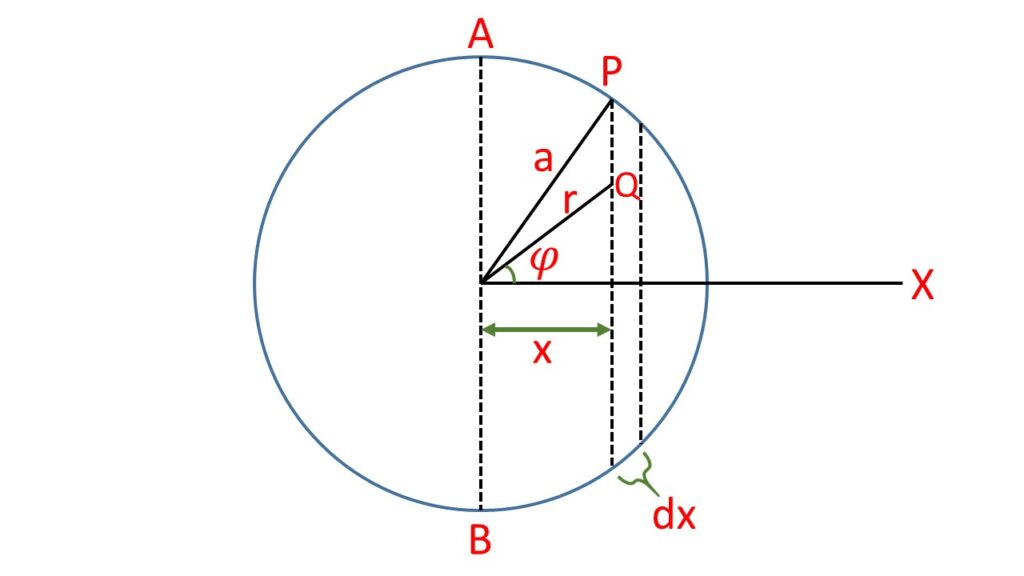

If \( \rho \) is the density of the material of the sphere.

Therefore the mass of the disc is \( \pi(a^2-x^2)\cdot\,dx\cdot\rho \).

At a point \( Q \), at a distance \( r \) from the centre of the sphere as shown in the adjoining Fig. 1,the gravitational intensity i.e, the gravitational intensity is \( F= G\frac{4}{3}\frac{\pi{r}^3\rho}{r^2}=G\frac{4}{3}\pi{r}\rho \)

Where \( G \) is the gravitational constant.

The component of the force \( F \) along the \( X-axis \) is

\( F\cos\phi=G\frac{4}{3}\pi{r}\rho\cdot\frac{x}{r}\\=G\frac{4}{3}\pi\rho{x} \)

Here the sine components cancel out due to the corresponding elements above and below of \( X-axis \).

Now for the all point masses on the strip, the cases are similar.

Hence the attraction force of the sphere on the elementary disc is,

\( G\frac{4}{3}\pi\rho\ \times\ \pi\rho(a^2-x^2)\,dx\\=\frac{4}{3}G{\pi}^2{\rho}^2{x}(a^2-x^2)\,dx \)

Now the total gravitational attraction between the two halves of the spheres divided by the diameter \( AB \) is

\( \frac{4}{3}G{\pi}^2{\rho}^2\displaystyle\int_0^a(a^2{x}-x^3)\,dx \\=\frac{4}{3}G{\pi}^2{\rho}^2\left[\frac{a^2{x}^2}{2}-\frac{x^4}{4}\right]_0^a \\=\frac{4}{3}G{\pi}^2{\rho}^2\left(\frac{a^4}{2}-\frac{a^4}{4}\right) \\=\frac{4}{3}G{\pi}^2{\rho}^2\frac{a^4}{4} \\=\frac{3}{16}G\frac{M^2}{a^2} \)

where,

\( M=\frac{4}{3}\pi{a^3}\rho\\ or,\ \rho=\frac{3M}{4\pi{a^3}}\\ or.\ {\rho}^2=\frac{9M^2}{16{\pi}^2{a^6}} \)