Motion of a body in a tunnel through the earth along a diameter:
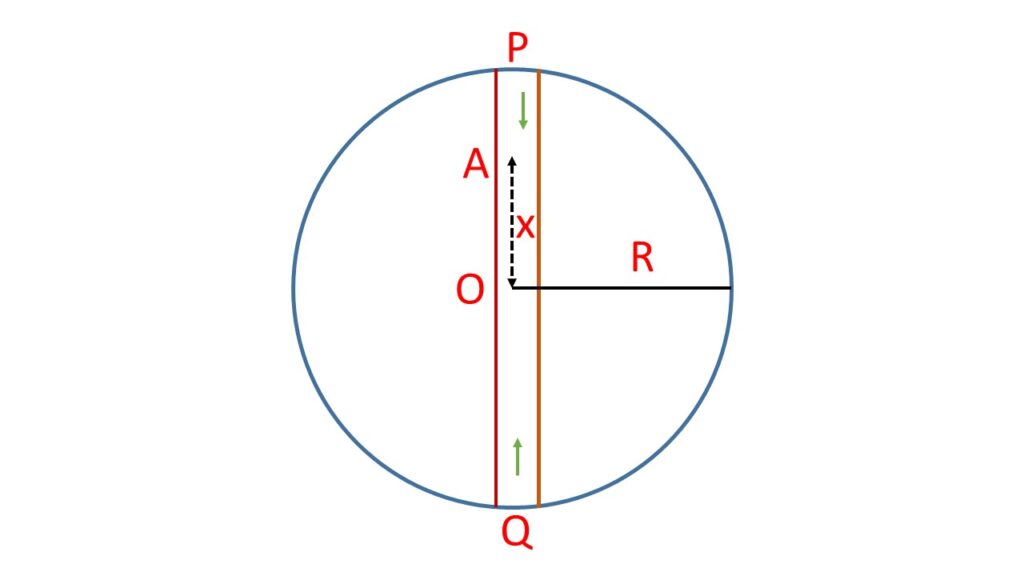
Let us consider the mass of the earth is \( M \) and the radius is \( R \) with centre at the point \( O \). A body of mass \( m \) is dropped into a frictionless straight tunnel \( PQ \), though the earth that is along a diameter as shown in the adjoining Fig. 1. \( \rho \) is the density of the earth.
At any instant of time the body is at the position \( A \), at a distance \( x \) from the centre of the earth \( O \).
Due to gravitational attraction, the force acting upon the body of mass \( m \) is only due to the inner solid sphere of radius \( x \). The shell external to it will have no influence on \( m \).
The force on \( m \) is given by,
\( F=-G\frac{\frac{4}{3}\pi{x^3}\rho{m}}{x^2}=-G\frac{4}{3}\pi{x}\rho{m} \)The negative sign indicates that, \( F \) and \( x \) are in the opposite direction to each other.
so we can write, \( F=-kx \), where \( k=G\frac{4}{3}\pi\rho{m} =\ constant\)
So here the force of attraction on the body is proportional to its distance from the centre and directed towards the centre of the earth. Therefore the motion of the body is a simple harmonic motion.
Time period of oscillation:
The differential equation of simple harmonic motion is,
\( m\frac{d^2{x}}{{dt}^2}=-kx \\or,\ \frac{d^2{x}}{{dt}^2}+\frac{k}{m}x=0\\ or,\ \frac{d^2{x}}{{dt}^2}+{\omega}^2{x}=0 \)Where, \( \omega=\sqrt{\frac{k}{m}}=\sqrt{G\frac{4}{3}\pi\rho} \)
Now the time period of this simple harmonic motion is,
\( T=\frac{2\pi}{\omega}=\frac{2\pi}{ \sqrt{G\frac{4}{3}\pi\rho} }\\ =\sqrt{\frac{3\pi}{G\rho}}\\=\sqrt{\frac{3\pi{4}\pi{R}G}{G3g}} \)or, \( \displaystyle{T=2\pi\sqrt{\frac{R}{g}}} \)
Where, the acceleration due to gravity on the earth’s surface is,
\( g=\frac{GM}{R^2}=G\frac{\frac{4}{3}\pi{R}^3\rho{M}}{R^2} \\=G\frac{4}{3}\pi{R}\rho \)or, \( \rho=\frac{3g}{4\pi{R}G} \).
