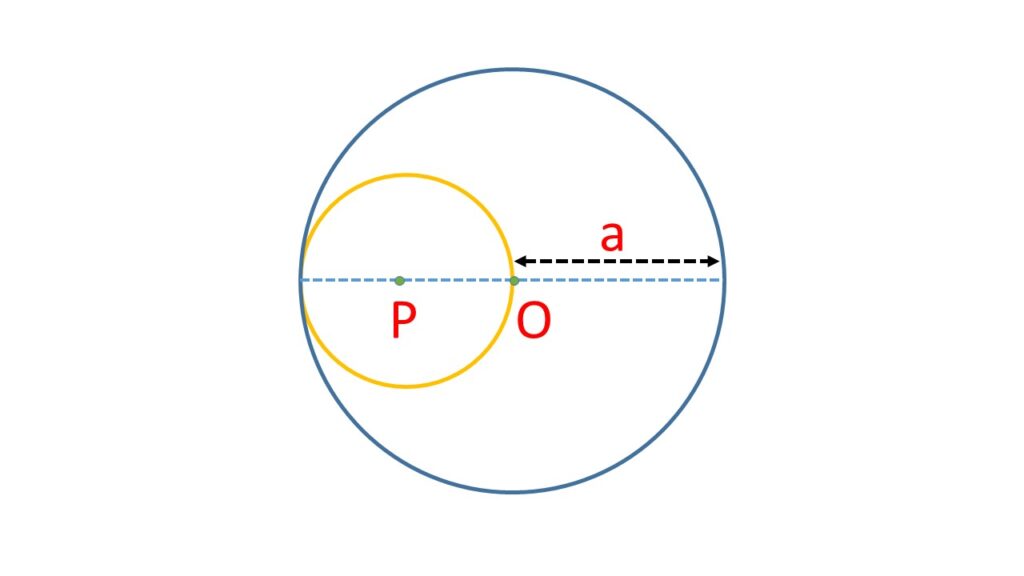
Let us consider a sphere of radius “a” with centre at “O” and a smaller sphere is described on the radius of the previous sphere as diameter with centre at “P”.
So the gravitational intensity at the point \( P \) within the large sphere is of magnitude
\( \displaystyle{f=G\cdot\frac{\frac{4}{3}\pi{(OP)}^3\sigma}{{(OP)}^2}\\ =G\cdot\frac{4}{3}\pi{(OP)}\sigma} \).
Where \( \sigma \) is the density of the material of the sphere.
Hence the portion included in the smaller sphere will be acted upon by the force given by,
\( F=G\cdot\frac{4}{3}\pi{(OP)}\sigma \times\)(mass of the smaller sphere)
\( F= G\frac{4}{3}\pi{(\frac{a}{2})}\sigma \times\frac{4}{3}\pi{(\frac{a}{2})}^3\sigma \\={(\frac{4}{3})}^2 {G}{\pi}^2{\sigma}^2{(\frac{a}{2})}^4 \\=\frac{1}{9}G{\pi}^2{\sigma}^2{(\frac{a}{2})}^4 \)or, \( F=\frac{1}{9}\cdot{G}{\pi}^2\frac{9M^2}{16{\pi}^2{a}^6}{a}^4 \\=\frac{1}{16}G\frac{M^2}{a^2} \)
Where, \( M=\frac{4}{3}\pi{a^3}\sigma\\or,\ {\sigma}^2=\frac{9M^2}{16{\pi}^2{a}^6} \)
