Internal Bending Moment:
A homogeneous beam is fixed at one end and is loaded at the other end. As a result, bending is produced in the beam.
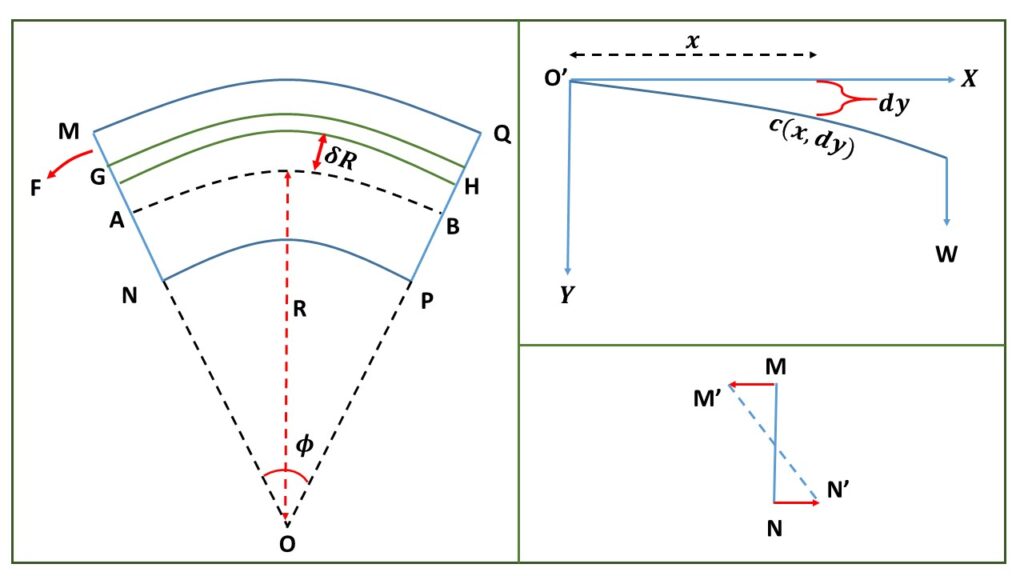
Let us consider, a homogeneous, isotropic, and uniform beam of length \( l \). This beam is fixed at the end \( O’ \) and is loaded at the other end by \( W \) as shown in the above figure. Now let us consider any arbitrary point \( c(x,dy) \) on the bending beam at a distance \( x \) from the fixed end \( O’ \). There is a small segment \( MNPQ \) around \( c \). When the beam is bent, the convex surface \( MN \) is stretched while the concave surface \( PN \) is compressed. There is an intermediate layer \( AB \) in between these surfaces, which maintains its original length. This layer \( AB \) is called neutral layer.
Let \( R \) be radius of curvature of his neutral layer. The segment \( MNPQ \) makes an angle \( \phi \) at the centre of curvature \( O \).
There is an elementary layer \( GH \) at a distance \( (R+\delta{R}) \) from the centre of curvature \( O \). The cross sectional area of this elementary layer is \( \alpha \).
Since the bending is small, so we can write
\( AB=R\phi \) and \( GH=(R+\delta{R})\phi \).
So the linear extension of the layer \( GH \) with respect to the neutral layer \( AB \) is \( (R+\delta{R})\phi-R\phi=\delta{R}\phi \)
Therefore the extensional stress is given by,
\( \frac{Extension\ in\ length}{Oroinal\ length}\\=\frac{\delta{R}\phi}{R\phi}\\=\frac{\delta{R}}{R} \).
Similarly we can write, there is a linear compressive strain at a distance \( \delta{R} \) below the neutral layer \( -\frac{\delta{R}}{R} \).
Corresponding to each of these strains there are stresses on the different layers. The forces act in the upper half \( MABQ \), produce elongation and the forces act in the lower half \( ANPB \), produce contractions. These two forces act in the opposite directions perpendicular to the section \( MNPQ \) and constitute a couple and the moment of this couple is called internal bending moment.
If \( F \) be the force acting perpendicular to the area \( \alpha \) then Young’s modulus
\( \displaystyle{Y=\frac{\frac{F}{\alpha}}{\frac{\delta{R}}{R}}\\=\frac{fR}{\alpha{\delta{R}}}} \)Therefore, \( \displaystyle{F=\frac{Y\cdot\alpha\cdot\delta{R}}{R}} \)
The moment of this force \( F \) about the neutral layer is
\( \displaystyle{F\delta{R}=\frac{Y\cdot\alpha\cdot{\delta{R}}^2}{R}} \)The total moment of all internal stress forces acting over the whole cross-section of the beam, i.e., the total internal bending moment is given by,
\(\displaystyle{ \frac{Y}{R}\sum\alpha{\delta{R}}^2\\=\frac{Y}{R}AK^2=\frac{Y}{R}I} \)Where \( I=AK^2 \) is the geometrical moment of inertia of the beam, \( A \) is the total cross-sectional area of the beam, \( K \) is the radius of gyration.
The quantity \( YI=YAK^2 \) is called the flexural rigidity. It is defined as the external bending moment required to produce a unit radius of curvature.
CASE I:
If the beam has a rectangular cross-section and the area of the cross-section is \( A=bd \), where \( b \) and \( d \) are the breadth and depth of the beam respectively. Then K^2=\frac{d^2}{12}.
Therefore the internal bending moment of the beam is, \( \frac{Y}{R}\cdot{bd}\cdot\frac{d^2}{12}=\frac{Ybd^3}{12R} \).
CASE II:
If the beam has a circular cross-section of area \( A=\pi{r^2} \), where \( r \) is the radius of the cross section and \( K^2=\frac{r^2}{4} \).
Therefore the internal bending moment of the ebam is \( \frac{Y}{R}\cdot\pi{r^2}\cdot\frac{r^2}{4}=\frac{Y\pi{r^4}}{4R} \)