Cantilever:
A beam of uniform cross-section ( circular or rectangular ) and of homogeneous, isotropic, elastic material fixed horizontally at one end and loaded at other free end is called cantilever.
The depression of the loaded end of a light cantilever:
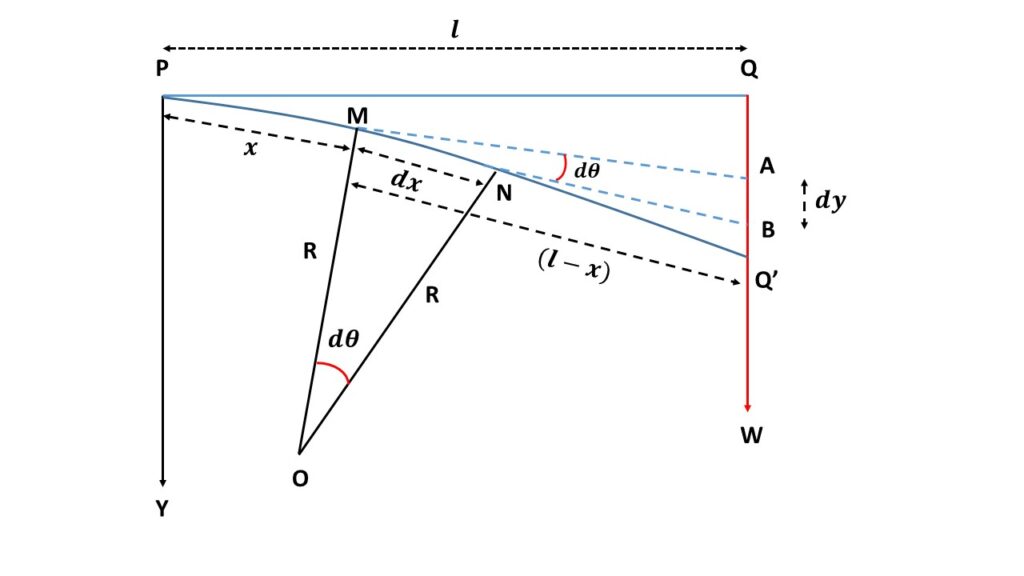
Let us consider, a light cantilever \( PQ \) of length \( l \) is fixed horizontally at the point \( P \). When a load \( W \) is added to its free end \( Q \), then the end \( Q \) is depressed to new position \( Q' \).
Let us consider a section on the beam at the point \( M \) at a distance \( x \) from the fixed end \( P \)
Since the point \( Q' \) is almost very close to the end \( Q \), so \( MQ' \) is almost perpendicular to \( QW \).
Therefore the moment of the external couple due to the load \( W \) is \( W\cdot(l-x) \).
Again we know that the internal bending moment is
\( \displaystyle{\frac{YI}{R}} \). [Read In Detail]
Where, \( R \) is the radius of curvature of the neutral axis at point \( P \), \( I \) is the geometrical moment of inertia of the beam, and \( Y \) is Young’s modulus of the material of the beam.
Now in the equilibrium of the beam, the external bending moment is balanced by the internal bending moment, So we can write
\( \frac{YI}{R}=W(l-x) \)
\( or,\ \displaystyle{\frac{1}{R}=\frac{W(l-x)}{YI}}\tag{1} \)
Let us consider another point \( N \) at a very close distance \( dx \) from the point \( M \) on the beam. Since \( dx \) is very small then the radius of curvature of the point \( N \) is also \( R \).
If \( \angle{MON}=d\theta \) then we can write, \( MN=R{d\theta}=dx \).
\( or,\ \displaystyle{\frac{1}{R}=\frac{d\theta}{dx}}\tag{2} \)
From equations (1) and (2),
\( \displaystyle{\frac{d\theta}{dx}=\frac{W(l-x)}{YI}} \)
Let us draw the tangents at \( M \) and \( N \) meeting the vertical line at \( A \) and \( B \) respectively.
The depression of \( N \) below \( M \) is
\( AB=dy=(l-x)d\theta \) , since the point M and N are very close to each other.
Using equation (3), we can write
\( \displaystyle{dy=(l-x)\cdot\frac{W(l-x)}{YI}dx\\=\frac{W{(l-x)}^2}{YI}dx} \)
Now the total depression of the cantilever is
\( \displaystyle{QQ'=y=\int_0^l{\frac{W{(l-x)}^2}{YI}dx}\\=\frac{W}{YI}\int_0^l{l^2+x^2-2lx}dx\\=\frac{W}{YI}{[l^2{x}+\frac{x^3}{3}-2l\frac{x^2}{2}]}_0^l\\=\frac{W}{YI}[l^3+\frac{l^3}{3}-l^3]} \)
\( or,\ \displaystyle{y=\frac{Wl^3}{3YI}} \)
CASE I :
For a beam of circular cross-section of radius \( r \),
The geometrical moment of inertia of the beam is \( I=\frac{\pi{r^4}}{4} \).
Therefore, \( \displaystyle{y=\frac{4Wl^3}{3Y\pi{r^4}}} \).
CASE II :
For a beam of rectangular cross section,
the moment of inertia of the beam is \( I=\frac{bd^3}{12} \),
where \( b \) is the breadth and \( d \) is the depth of the beam.
Therefore, \( \displaystyle{y=\frac{4Wl^3}{Ybd^3}} \)
