Ans.

Let us consider a system of two particles of masses \( m_1 \) and \( m_2 \) having position vectors \( \vec{r_1} \) and \( \vec{r_2} \) respectively with respect to the origin O as shown in the Fig. 1.

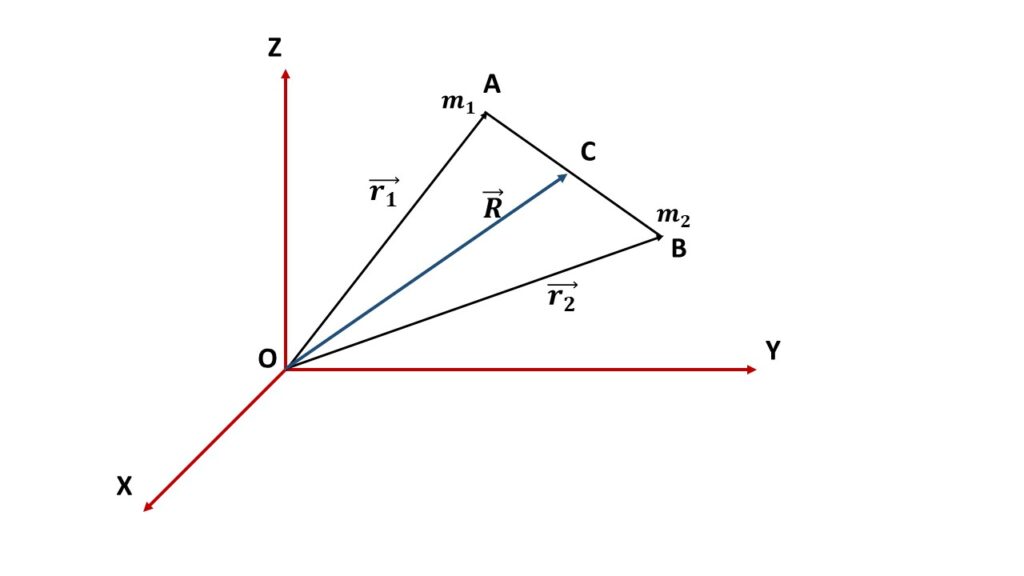
The centre of mass C of this system having position vector \( \vec{R} \) is given by

\( \displaystyle{\vec{R}=\frac{m_1\vec{r_1}+m_2\vec{r_2}}{m_1+m_2}} \)

If the centre of mass lies at the origin O of the coordinate system, then

\( \vec{R}=0 \)

or, \( m_1\vec{r_1}+m_2\vec{r_2}=0 \)

or, \( m_1\vec{r_1}=-m_2\vec{r_2} \)

or, \( \frac{m_1}{m_2}=-\frac{\vec{r_2}}{\vec{r_1}} \)

Thus the centre of mass divides the line joining the two masses in the inverse ratio of their masses. It should be noted that if O is the origin and \( \vec{r_2} \) is positive then \( \vec{r_1} \) must be negative.