Ans.

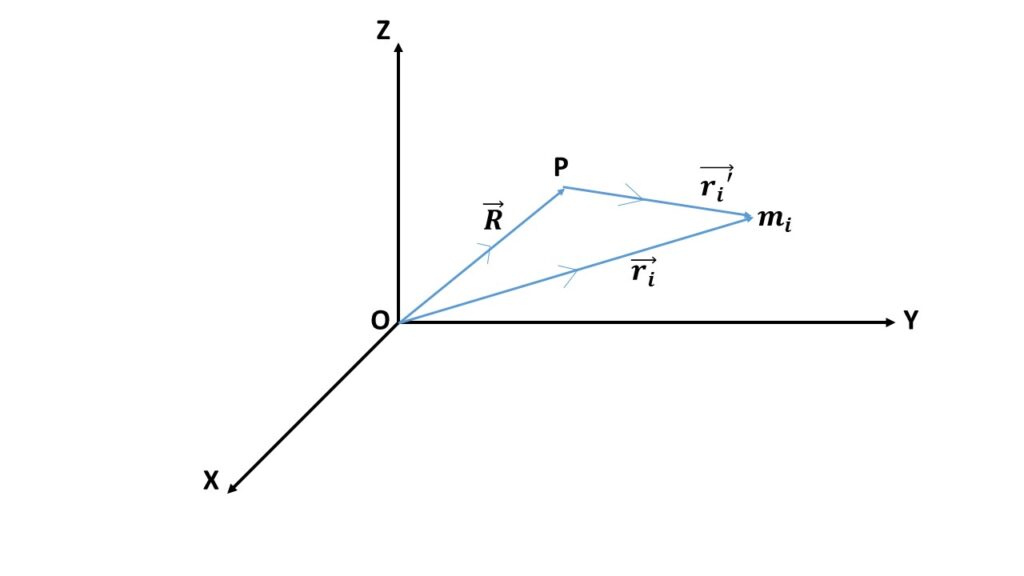
Let us consider a system of n particles of masses \( m_1 \), \( m_2 \), \( \cdots \), \( m_n \) having position vector \( \vec{r_1} \), \( \vec{r_2} \), \( \cdots \), \( \vec{r_n} \) with respect to the origin O. Let P be the centre of mass of the system having position vector \( \vec{R} \) with respect to the origin O is given by,

\( \vec{R}=\frac{1}{M}\displaystyle{\sum_{i=1}^{n}m_i\vec{r_i}}\tag{1} \)

where, \( \vec{r_i} \) is the position vector of the ith particle of mass \( m_i \), and \( \displaystyle{M=\sum_{i=1}^{n}m_i} \) is the total mass of the system.

Let, \( \vec{r_i}' \) be the position vector of the ith particle of mass \( m_i \) with respect to the centre of mass point P, then from Fig. 1 we can write,

\( \vec{r_i}=\vec{R}+\vec{r_i}'\tag{2} \)

differentiating both side with respect to the time t, we get

\( \frac{d\vec{r_i}}{dt}=\frac{d\vec{R}}{dt}+\frac{d\vec{r_i}'}{dt} \)

or, \( \vec{v_i}=\vec{V}+\vec{v_i}'\tag{3} \)

Where, \( \vec{V} \) is the velocity of the centre of mass P with respect to the origin O, \( \vec{v_i} \) is the velocity of the ith particle with respect to the origin O and \( \vec{v_i}' \) is the velocity of the ith particle with respect to the centre of mass point P.

So the total angular momentum of the system relative to the origin O is given by,

\( \vec{L}=\displaystyle{\sum_{i=1}^{n}}m_i(\vec{r_i}\times\vec{v_i}) \)

= \( \displaystyle{\sum_{i=1}^{n}}m_i[(\vec{R}+\vec{r_i}')\times(\vec{V}+\vec{v_i}')] \)

= \( \displaystyle{\sum_{i=1}^{n}}m_i[\vec{R}\times\vec{V}]+\vec{R}\times[\displaystyle{\sum_{i=1}^{n}}m_i\vec{v_i}']+[\displaystyle{\sum_{i=1}^{n}}m_i\vec{r_i}']\times\vec{V}+\displaystyle{\sum_{i=1}^{n}}m_i[\vec{r_i}'\times\vec{v_i}'] \)

= \( M(\vec{R}\times\vec{V})+\displaystyle{\sum_{i=1}^{n}}m_i[\vec{r_i}'\times\vec{v_i}'] \)

Where, \( \displaystyle{\sum_{i=1}^{n}}m_i\vec{v_i}'=0 \) and \( \displaystyle{\sum_{i=1}^{n}}m_i\vec{r_i}'=0 \)

So the total angular momentum of the system of particles about any point is equal to the angular momentum of the centre of mass about that point plus the angular momentum of the system about the centre of mass.