Let us consider a point A in a three-dimensional Cartesian co-ordinate system, the position of this point can be described by a specific single vector. This vector is the displacement of that point A with respect to the origin O of the co-ordinate system, as shown in the figure below.

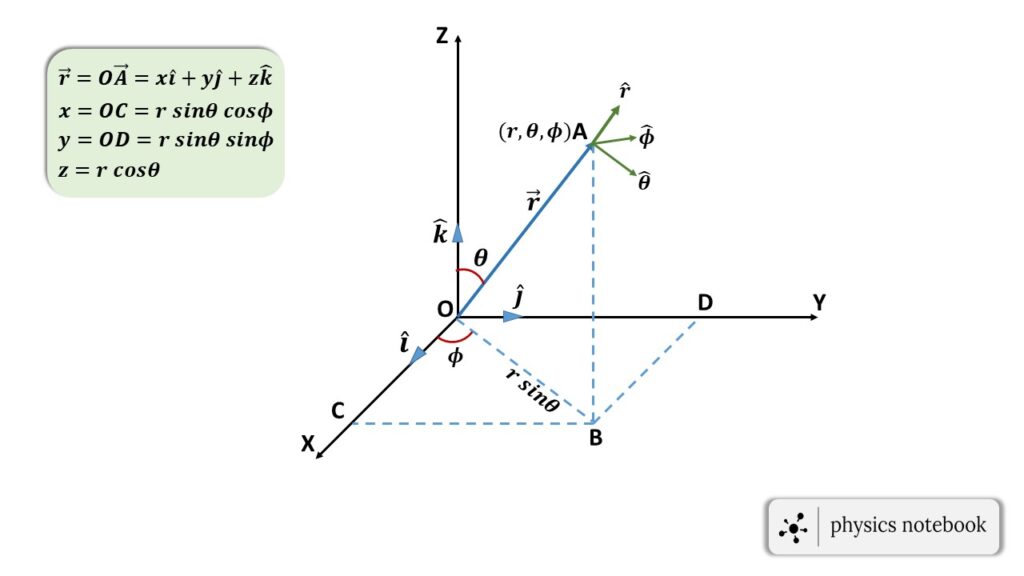
This vector is known as the “position vector” of that point A with respect to the origin O.

Here the position vector is denoted by the \( \vec{OA}=\vec{r} \).

\( \vec{r} \) gives the magnitude as well as the direction of displacement.

If \( \hat{r} \) be the unit vector along \( \vec{r} \), then we can write,

\( \displaystyle{\hat{r}=\frac{\vec{r}}{|\vec{r}|}} \). where, \( |\vec{r}| \) is the magnitude of the vector \( \vec{r} \).

Let, \( (r,\theta,\phi) \) be the spherical polar co-ordinates of the point A with respect to the origin O and  \( (x,y,z) \) be the corresponding cartesian co-ordinates of that point A as shown in the figure 1.

therefore, \( \vec{r}=x\hat{i}+y\hat{j}+z\hat{k} \)

where, \( \hat{x},\ \hat{i},\) & \( \hat{k} \) are the unit vectors along the X-axis, Y-axis and Z-axis respectively.

\( x=r\sin\theta\ \cos\phi \)

\( y=r\sin\theta\ \sin\phi \)

and \( z=r\cos\theta \).

So the displacement can be written as,

\( \vec{r}= r\sin\theta\ \cos\phi\ \hat{i}+ r\sin\theta\ \sin\phi\ \hat{j}+ r\cos\theta\ \hat{k}\tag{1} \)

The unit vector \( \hat{r} \) can be written as,

\( \hat{r}= \sin\theta\ \cos\phi\ \hat{i}+ \sin\theta\ \sin\phi\ \hat{j}+ \cos\theta\ \hat{k}\tag{2} \)

Let, \( \hat{\theta} \) be the unit vector in the direction of increasing \( \theta \) and perpendicular to the unit vector \( \hat{r} \)

And \( \hat{\phi} \) be the unit vector along the direction of increasing \( \phi \) and perpendicular to both the unit vectors \( \hat{r} \) and \( \hat{\theta} \),

then we can write,

\( \hat{\theta}=\cos\theta\ \cos\phi\ \hat{i}+\cos\theta\ \sin\phi\ \hat{j}-\sin\theta\ \hat{k}\tag{3} \)

\( \hat{\phi}=-\sin\phi\ \hat{i}+\cos\phi\ \hat{j}\tag{4} \) [to know the derivation for the unit vectors \( \hat{\theta} \) and \( \hat{\phi} \) in term of \( \hat{i} \), \( \hat{j} \), \( \hat{k} \) (CLICK HERE)]

Velocity in spherical polar co-ordinate:

Since the velocity is the time derivative of the displacement,

Then, Velocity \( \displaystyle{\vec{v}=\frac{d\vec{r}}{dt}} \)

\( or,\ \displaystyle{\vec{v}=\frac{d}{dt}(r\hat{r})=\frac{dr}{dt}\hat{r}+r\frac{d\hat{r}}{dt}}\tag{5} \)

Using equation (2) we get,

\( \displaystyle{\frac{d\hat{r}}{dt}=\frac{d}{dt}(\sin\theta\ \cos\phi\ \hat{i}+ \sin\theta\ \sin\phi\ \hat{j}+ \cos\theta\ \hat{k})} \)

\( or,\ \displaystyle{\frac{d\hat{r}}{dt}=(\cos\theta\ \cos\phi\ \frac{d\theta}{dt}-\sin\theta\ \sin\phi\ \frac{d\phi}{dt})\hat{i}+(\cos\theta\ \sin\phi\ \frac{d\theta}{dt}+\sin\theta\ \cos\phi\ \frac{d\phi}{dt})\hat{j}-\sin\theta\ \frac{d\theta}{dt}\hat{k}} \)

\( or,\ \displaystyle{\frac{d\hat{r}}{dt}=(\cos\theta\ \cos\phi\ \dot{\theta}-\sin\theta\ \sin\phi\ \dot{\phi})\hat{i}+(\cos\theta\ \sin\phi\ \dot{\theta} +\sin\theta\ \cos\phi\ \dot\phi)\hat{j}-\sin\theta\ \dot{\theta} \hat{k}} \)

\( or,\ \displaystyle{\frac{d\hat{r}}{dt}=\dot{\theta}(\cos\theta\ \cos\phi\ \hat{i}+\cos\theta\ \sin\phi\ \hat{j}-\sin\theta\ \hat{k})+\dot{\phi}(-\sin\phi\ \hat{i}+\cos\phi\ \hat{j})\ \sin\theta} \)

\( or,\ \displaystyle{\frac{d\hat{r}}{dt}=\dot{\theta}\ \hat{\theta}+\dot{\phi}\ \hat{\phi}\ \sin\theta} \)

[ Using equations (3) and (4) ]

Putting the value of \( \frac{d\hat{r}}{dt} \) in equation (5), we get,

\( \displaystyle{\vec{v}=\frac{dr}{dt}\hat{r}+r\frac{d\hat{r}}{dt}} \)

\( or,\ \vec{v}=\dot{r}\ \hat{r}+r\ \dot{\theta}\ \hat{\theta}+r\ \dot{\phi}\ \hat{\phi}\ \sin\theta\tag{6} \)

Components of the velocity in spherical polar co-ordinate:

Equation (6) can be written as,

\( \displaystyle{\vec{v}=\vec{v_r}+\vec{v_{\theta}}+\vec{v_{\phi}}} \)

where, \( \vec{v_r} \) is the velocity along the \( \vec{r} \),

\( \vec{v_{\theta}} \) is the velocity along \( \theta \),

and \( \vec{v_{\phi}} \) is the velocity along \( \phi \).

These three velocity vector components are orthogonal to each other in the spherical polar co-ordinate system.

The magnitude of this velocity vector is,

\( |\vec{v}|=\sqrt{{\dot{r}}^2+{r}^2\ {\dot{\theta}}^2+r^2\ {\dot{\phi}}^2\ {\sin}^2\theta} \)