The expression for the velocity of a particle in the spherical polar co-ordinate system is,

\( \vec{v}=\dot{r}\ \hat{r}+r\ \dot{\theta}\ \hat{\theta}+r\ \dot{\phi}\ \hat{\phi}\ \sin\theta\tag{1} \)

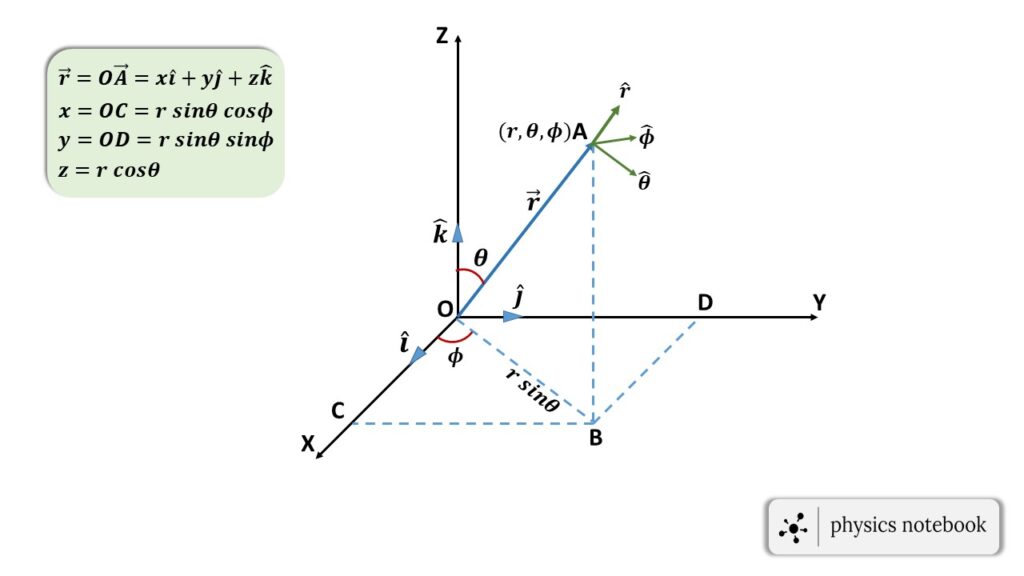
where, \( \hat{r} \), \( \hat{\theta} \) & \( \hat{\phi} \) are the unit vectors in the spherical polar co-ordinate system.

[ To know the derivation for the expression for the velocity in spherical polar co-ordinate system (CLICK HERE) ]

Expression for acceleration in spherical polar coordinate:

Now acceleration is the time derivative of velocity,

Therefore, acceleration \( \displaystyle{\vec{a}=\frac{d\vec{v}}{dt}} \)

\( or,\ \displaystyle{\vec{a}=\frac{d}{dt}(\dot{r}\ \hat{r}+r\ \dot{\theta}\ \hat{\theta}+r\ \dot{\phi}\ \hat{\phi}\ \sin\theta)} \)

\( or,\ \vec{a}=\ddot{r}\hat{r}+\dot{r}\frac{d\hat{r}}{dt}+\dot{r}\dot{\theta}\hat{\theta}+r\ddot{\theta}\hat{\theta}+r\dot{\theta}\frac{d\hat{\theta}}{dt}+\dot{r}\dot{\phi}\hat{\phi}\ \sin\theta+r\dot{\phi}\hat{\phi}\ (\cos\theta)\ \dot{\theta}+r\ddot{\phi}\hat{\phi}\ \sin\theta+r\dot{\phi}\frac{d\hat{\phi}}{dt}\ \sin\theta\tag{2} \)

Now we know that,

\( \hat{r}=\sin\theta\ \cos\phi\ \hat{i}+\sin\theta\ \sin\phi\ \hat{j}+\cos\theta\ \hat{k}\tag{i} \) \( \hat{\theta}=\cos\theta\ \cos\phi\ \hat{i}+\cos\theta\ \sin\phi\ \hat{j}-\sin\theta\ \hat{k}\tag{ii} \) \( \hat{\phi}=-\sin\phi\ \hat{i}+\cos\phi\ \hat{j}\tag{iii} \)

[ To know the derivation for the expression of unit vectors in the spherical polar co-ordinate system in terms of the unit vectors in thee-dimensional cartesian co-ordinate system (CLICK HERE) ]

The derivative of unit vector \( \hat{r} \) with respect to time t is,

\( \frac{d\hat{r}}{dt}=\frac{d}{dt}(\sin\theta\ \cos\phi\ \hat{i}+\sin\theta\ \sin\phi\ \hat{j}+\cos\theta\ \hat{k}) \)

\( or,\ \frac{d\hat{r}}{dt}=(\cos\theta\cos\phi\frac{d\theta}{dt}-\sin\theta\sin\phi\frac{d\phi}{dt})\hat{i}+(\cos\theta\sin\phi\frac{d\theta}{dt}+\sin\theta\cos\phi\frac{d\phi}{dt})\hat{j}-(\sin\theta\frac{d\theta}{dt})\hat{k} \)

\( or,\ \frac{d\hat{r}}{dt}=(\cos\theta\cos\phi\dot{\theta}-\sin\theta\sin\phi\dot{\phi})\hat{i}+(\cos\theta\sin\phi\dot{\theta}+\sin\theta\cos\phi\dot{\phi})\hat{j}-(\dot{\theta}\sin\theta)\hat{k} \)

\( or,\ \frac{d\hat{r}}{dt}=\dot{\theta}(\cos\theta\cos\phi\hat{i}+\cos\theta\sin\phi\hat{j}-\sin\theta\hat{k})+\dot{\phi}(-\sin\phi\hat{i}+\cos\phi\hat{j})\sin\theta \)

\( or,\ \frac{d\hat{r}}{dt}=\dot{\theta}\hat{\theta}+\dot{\phi}\hat{\phi}\sin\theta \)

The derivative of unit vector \( \hat{\theta} \) with respect to time is,

\( \frac{d\hat{\theta}}{dt}=\frac{d}{dt}(\cos\theta\ \cos\phi\ \hat{i}+\cos\theta\ \sin\phi\ \hat{j}-\sin\theta\ \hat{k}) \)

\( or,\ \frac{d\hat{\theta}}{dt}=(-\sin\theta\frac{d\theta}{dt}\cos\phi-\cos\theta\sin\phi\frac{d\phi}{dt})\hat{i}+(-\sin\theta\frac{d\theta}{dt}\sin\phi+\cos\theta\cos\phi\frac{d\phi}{dt})\hat{j}-(\cos\theta\frac{d\theta}{dt})\hat{k} \)

\( or,\ \frac{d\hat{\theta}}{dt}=(-\dot{\theta}\sin\theta\cos\phi-\dot{\phi}\cos\theta\sin\phi)\hat{i}+(-\dot{\theta}\sin\theta\sin\phi+\dot{\phi}\cos\theta\cos\phi)\hat{j}-\dot{\theta}\cos\theta\hat{k} \)

\( or,\ \frac{d\hat{\theta}}{dt}=-\dot{\theta}(\sin\theta\cos\phi\hat{i}+\sin\theta\sin\phi\hat{j}+\cos\theta\hat{k})+\dot{\phi}(-\sin\theta\hat{i}+\cos\theta\hat{j})\cos\theta \)

\( or,\ \frac{d\hat{\theta}}{dt}=-\dot{\theta}\hat{r}+\dot{\phi}\hat{\phi}\cos\theta \)

The derivative of unit vector \( \hat{\phi} \) with respect to time is,

\( \frac{d\hat{\phi}}{dt}=\frac{d}{dt}(-\sin\phi\ \hat{i}+\cos\phi\ \hat{j}) \)

\( or,\ \frac{d\hat{\phi}}{dt}=(-\cos\phi\frac{d\phi}{dt}\hat{i}-\sin\phi\frac{d\phi}{dt}\hat{j}) \)

\( or,\ \frac{d\hat{\phi}}{dt}=(-\dot{\phi}\cos\phi\hat{i}-\dot{\phi}\sin\phi\hat{j}) \)

\( or,\ \frac{d\hat{\phi}}{dt}=-\dot{\phi}(\cos\phi\hat{i}+\sin\phi\hat{j}) \)

\( or,\ \frac{d\hat{\phi}}{dt}=-\dot{\phi}(\sin\theta\hat{r}+\cos\theta\hat{\theta}) \)

Putting the value of \( \frac{d\hat{r}}{dt} \), \( \frac{d\hat{\theta}}{dt} \), \( \frac{d\hat{\phi}}{dt} \) in equation (2) we get,

\( \vec{a}=\ddot{r}\hat{r}+\dot{r}\dot{\theta}\hat{\theta}+\dot{r}\hat{\phi}(\sin\theta)\hat{\phi}+\dot{r}\dot{\theta}\hat{\theta}\\+r\ddot{\theta}\hat{\theta}-r{\dot{\theta}}^2\hat{r}+r\dot{\theta}\dot{\phi}(\cos\theta)\hat{\phi}+\dot{r}\dot{\phi}(\sin\theta)\hat{\phi}\\+r\dot{\theta}\dot{\phi}(\cos\theta)\hat{\phi}+r\ddot{\phi}(\sin\theta)\hat{\phi}-r{\dot{\phi}}^2({\sin}^2\theta)\hat{r}-r{\dot{\phi}}^2(\sin\theta\cos\theta)\hat{\theta} \)

\( or,\ \vec{a}=(\ddot{r}-r{\dot{\theta}}^2-r{\dot{\phi}}^2{\sin}^2\theta)\hat{r}\\+(2\dot{r}\dot{\theta}+r\ddot{\theta}-r{\dot{\phi}}^2\sin\theta\ \cos\theta)\hat{\theta}\\+(2\dot{r}\dot{\phi}\sin\theta+2r\dot{\theta}\dot{\phi}\cos\theta+r\ddot{\phi}\sin\theta)\hat{\phi} \)

Components of acceleration in spherical polar co-ordinate:

The above equation can be written as,

\( \vec{a}=\vec{a_r}+\vec{a_{\theta}}+\vec{a_{\phi}} \)

where, \( \vec{a_r}=(\ddot{r}-r{\dot{\theta}}^2-r{\dot{\phi}}^2\ {\sin}^2\theta)\hat{r} \)

\( \vec{a_{\theta}}=(r\ddot{\theta}+2\dot{r}\dot{\theta}-r{\dot{\phi}}^2\ \sin\theta\ \cos\theta)\hat{\theta} \)

\( \vec{a_{\phi}}=(r\ddot{\phi}\sin\theta+2\dot{r}\dot{\phi}\sin\theta+2r\dot{\theta}\dot{\phi}\cos\theta)\hat{\phi} \)

Since the unit vectors \( \hat{r} \), \( \hat{\theta} \), \( \hat{\phi} \) are mutually perpendicular to each other, so the magnitude of the acceleration \( \vec{a} \) can be written as,

\( \displaystyle{|\vec{a}|=\sqrt{{|\vec{a_r}|}^2+{|\vec{a_{\theta}}|}^2+{|\vec{a_{\phi}}|}^2}} \)