Velocity of centre of mass:

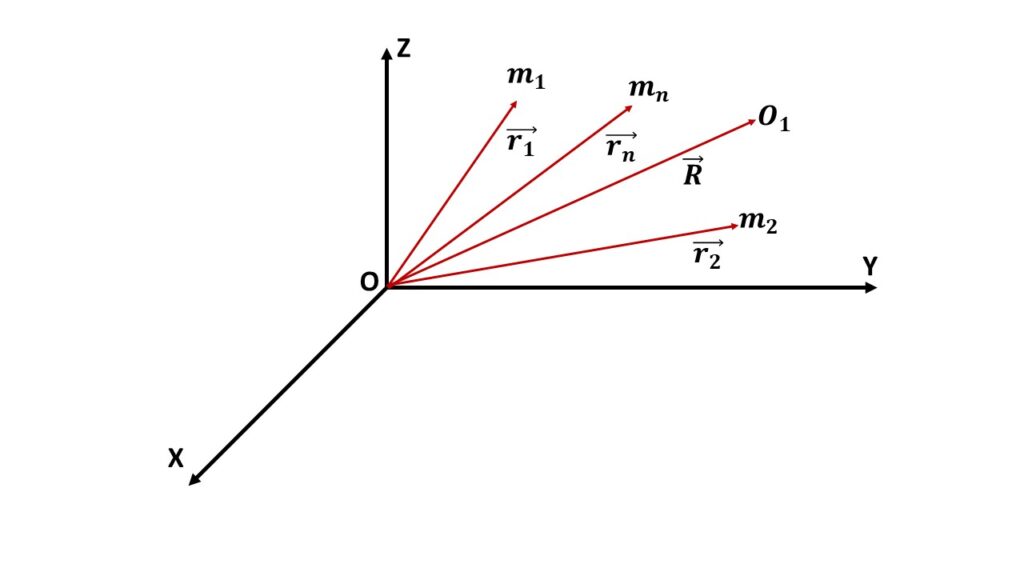
For a system of n particles of masses \( m_1 \), \( m_2 \), \( \cdots \), \( m_n \) having position vectors \( \vec{r_1} \), \( \vec{r_2} \), \( \cdots \), \( \vec{r_n} \) respectively with respect to the origin O, the centre of mass is defined by the point \( O_1 \) having position vector \( \vec{R} \) given by,

\( \vec{R}=\frac{1}{M}\displaystyle{\sum_{i=1}^{n}}m_ir_i \)

[Where \( M=\displaystyle{\sum_{i=1}^{n}}m_i \) is the total mass of the system.]

or, \( M\vec{R}=\displaystyle{\sum_{i=1}^{n}}m_ir_i \)

or, \( M\vec{R}=m_1\vec{r_1}+m_2\vec{r_2}+\cdots+m_n\vec{r_n}\tag{i} \)

Differentiating both side of equation (i) with respect to time, we get

\( M\frac{d\vec{R}}{dt}=m_1\frac{d\vec{r_1}}{dt}+m_2\frac{d\vec{r_2}}{dt}+\cdots+m_n\frac{d\vec{r_n}}{dt} \)

or, \( M\vec{V}=m_1\vec{v_1}+m_2\vec{v_2}+\cdots+m_n\vec{v_n} \)

So the velocity of the centre of mass of a system is

\( \vec{V}=\frac{1}{M}\displaystyle{\sum_{i=1}^{n}}m_i\vec{v_i}\tag{ii} \)

Acceleration of centre of mass:

Differentiating both side of equation (ii) with respect to time, we get

\( \frac{d\vec{V}}{dt}=\frac{1}{M}\left[m_1\frac{d\vec{v_1}}{dt}+m_2\frac{d\vec{v_2}}{dt}+\cdots+m_n\frac{d\vec{v_n}}{dt} \right] \)

or, \( \vec{a}=\frac{1}{M}\left[m_1\vec{a_1}+m_2\vec{a_2}+\cdots+m_n\vec{a_n} \right] \)

or, \( \vec{a}=\frac{1}{M}\displaystyle{\sum_{i=1}^{n}}m_i\vec{a_i}\tag{iii} \)