Angular Momentum:

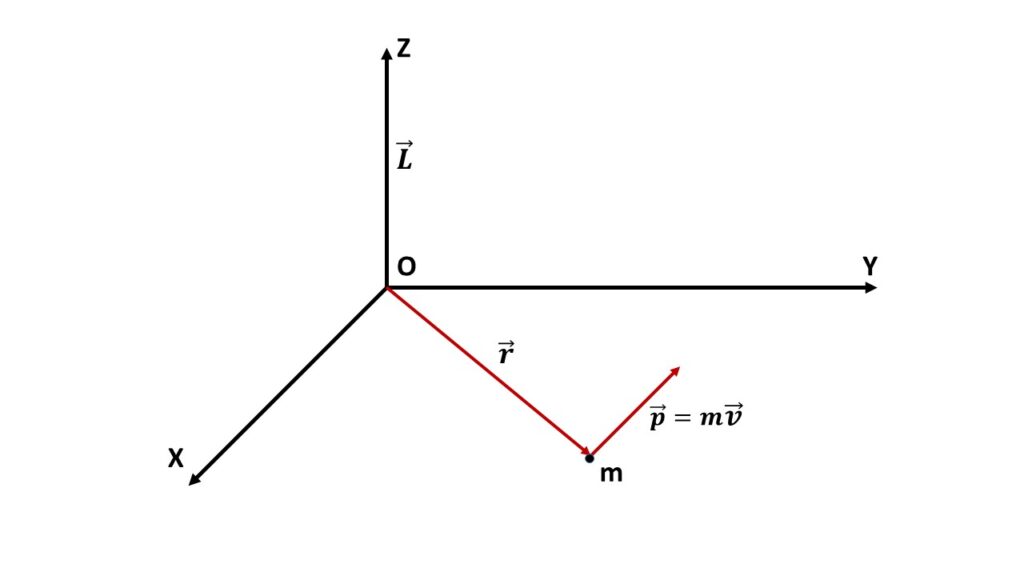
The angular momentum of a particle about a fixed point is defined by the moment of linear momentum of the particle about that fixed point.

If $\vec{r}$ be the position vector of a particle of mass $m$ with respect to the fixed point O and $\vec{p}$ be the linear momentum of that particle then, the angular momentum is defined by,

$\vec{L}=\vec{r}\times\vec{p}\tag{1}$

If the particle is moving with the velocity $\vec{v}$, then the linear momentum $\vec{p}=m\vec{v}$. So the equation (1) will be,

$\vec{L}=\vec{r}\times{m\vec{v}}\tag{2}$

The direction of $\vec{L}$ is perpendicular to the plane containing $\vec{r}$ and $\vec{v}$ or $\vec{p}$, according to the rule of right hand screw for the cross product of two vectors.

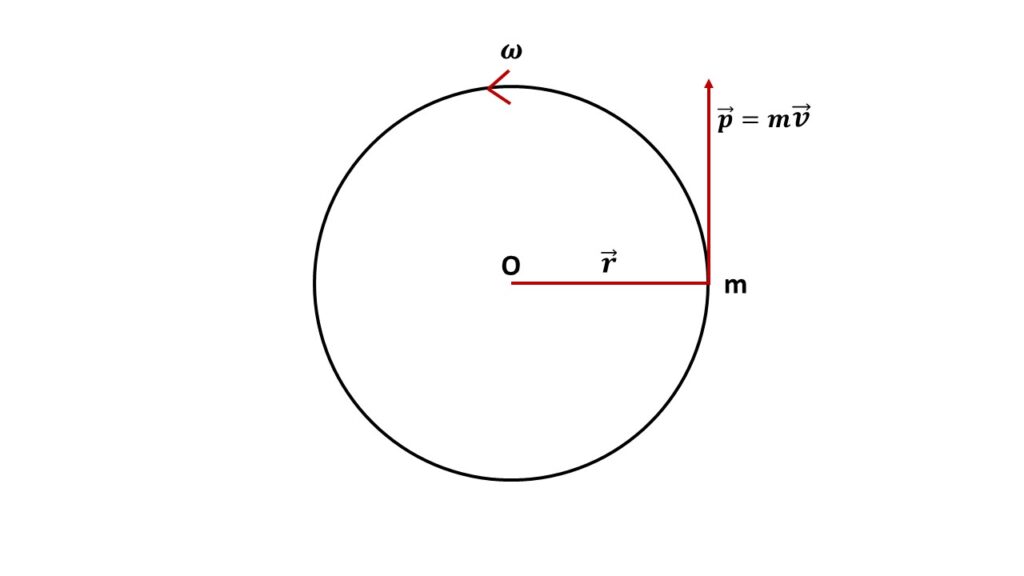
Let us consider particle of mass $m$ moves in a circular path of radius $r$ with angular velocity $\omega$, so we can write that the linear velocity $v=r\omega$. The angular momentum $\vec{L}=\vec{r}\times{m\vec{v}}$.

So the magnitude of angular momentum is

$|\vec{L}|=rmv=rm(r\omega)\\=mr^2\frac{d\theta}{dt}\\=mr^2\dot{\theta}$,

where $\theta$ is the angular displacement.

Torque:

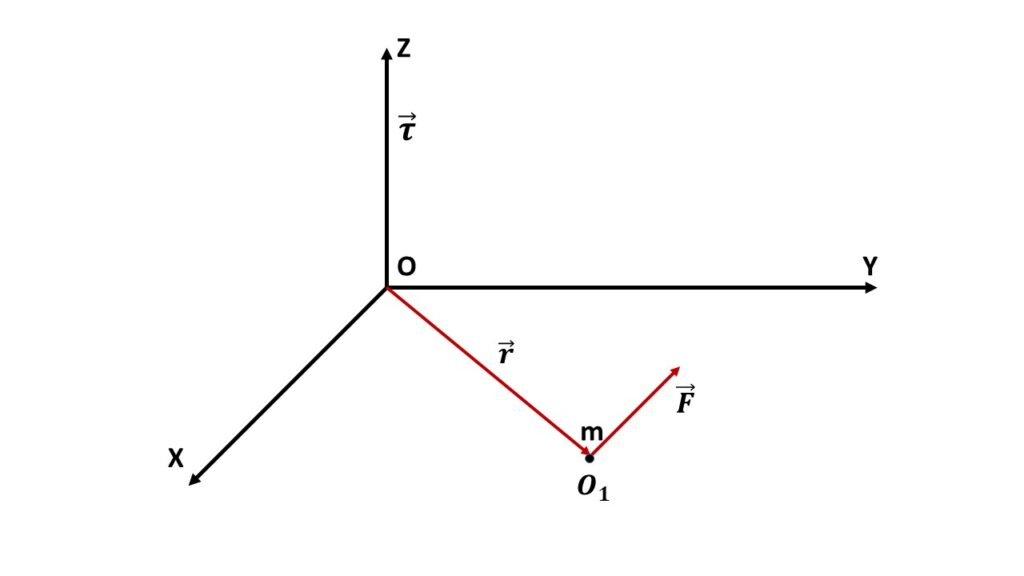
Let us consider $\vec{F}$ be the force acting on a particle of mass $m$ at the point $O_1$, whose position vector is $r$ with respect to the origin $O$.

Now the torque acting on this particle about the origin $O$ is defined as

$\vec{\tau}=\vec{r}\times\vec{F}$

The direction of the torque is normal to the plane containing $\vec{r}$ and $\vec{F}$, according to the right hand screw rule for the cross product of two vectors.