(i) Moment of inertia of a circular ring about an axis passing through its centre and perpendicular to the plane of the ring:

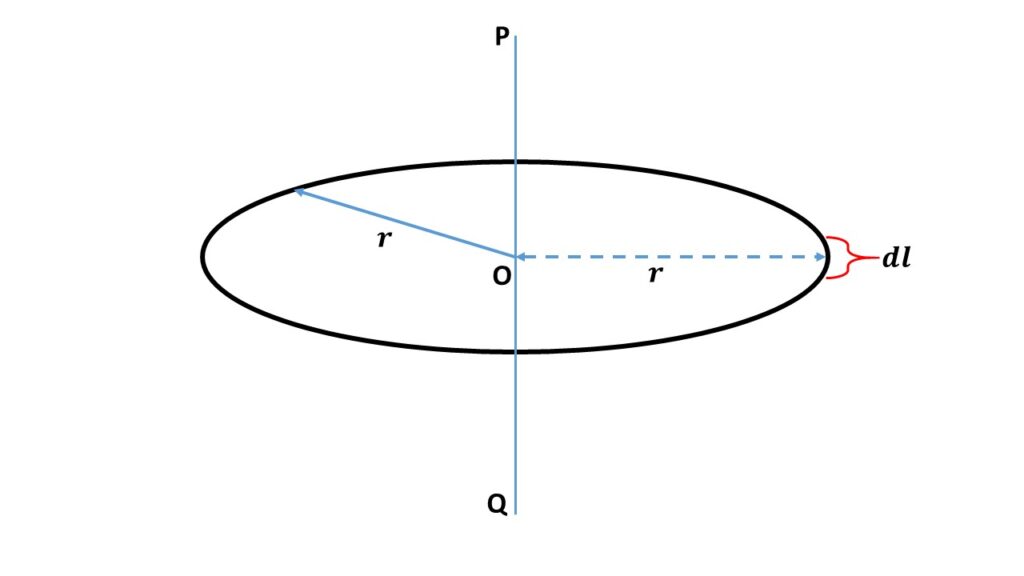
Let us consider a circular uniform ring of radius \( r \) and mass \( M \), rotating about an axis PQ passing through its centre \( O \) and perpendicular to the plane of the ring. So the length of this ring is \( 2\pi{r} \) and the mass density i.e., mass per unit length of this ring is \( \frac{M}{2\pi{r}} \). In order to calculate the moment of inertia of this ring about the axis \( PQ \), let us consider an elementary length \( dl \) on the ring, as shown in above Fig. 1. So the mass of this elementary length \( dl \) is \( \frac{M}{2\pi{r}}dl \). The moment of inertia of this elementary length \( dl \) about the axis \( PQ \) is \( \frac{M}{2\pi{r}}{r^2}dl \) = \( \frac{Mr}{2\pi}dl \).

So the moment of inertia of this whole ring about the axis \( PQ \) is

\( I=\frac{Mr}{2\pi}\sum{dl} \)

\( or,\ I=\frac{Mr}{2\pi}(2\pi{r}) \)

\( or,\ \displaystyle{I=Mr^2} \)

Moment of inertia of a circular ring about an axis passing through its centre and lying in the plane of the ring:

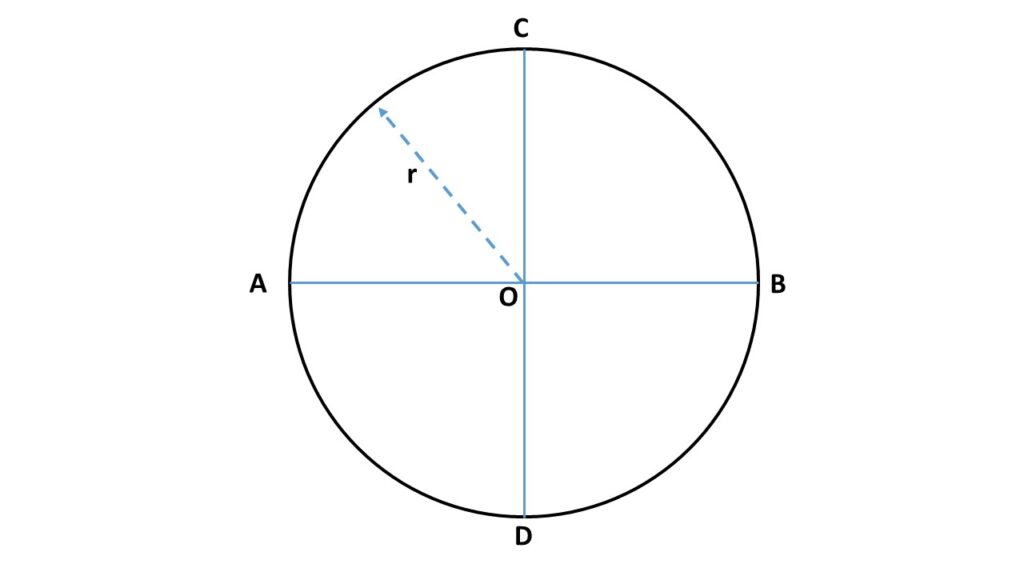
Let us consider two mutually perpendicular diameters AB and CD of the circular uniform ring of radius \( r \) and mass \( M \). If \( I_d \) be the moment of inertia about one diameter \( AB \), then the moment of inertia about another diameter \( CD \) will be the same i.e., will be \( I_d \). By applying the theorem of perpendicular axes, we can write

\( I_d+I_d=I \)

[ where \( I \) is the moment of inertia of the ring about the axis passing through the centre of this ring and perpendicular to the plane of the ring]

\( or,\ I_d=\frac{1}{2}I \)

\( or,\ \displaystyle{I_d=\frac{1}{2}Mr^2} \)