(i) Flow through capillary tubes in series combination :

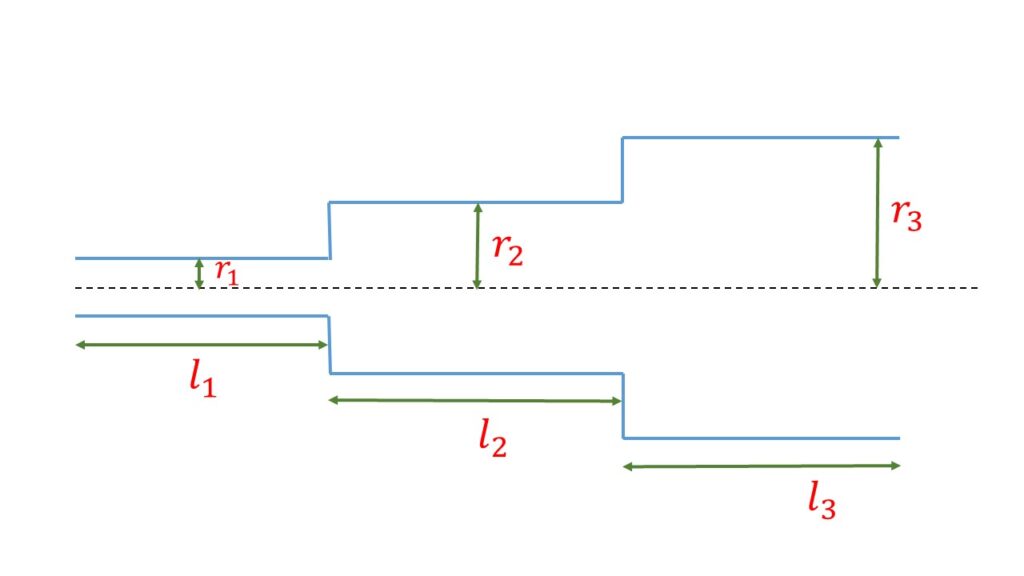
Let us consider a number of capillary tubes of radii \( r_1 \), \( r_2 \), \( r_3 \), \( \cdots \) of length \( l_1 \), \( l_2 \), \( l_3 \), \( \cdots \) respectively are joined in series as shown in the Fig. 1.

Let \( P_1 \), \( P_2 \), \( P_3 \), \( \cdots \) are the pressure difference between the entrance and exit ends of the tubes respectively.

Since the rate of flow of liquid in each capillary tube is same.

So we can write,

\( V= \frac{\pi{P_1}{r_1}^4}{8\eta{l_1}}= \frac{\pi{P_2}{r_2}^4}{8\eta{l_2}}= \cdots \)

Therefore,

\( P_1=\frac{8\eta{l_1}}{\pi{r_1}^4}V \),

\( P_2= \frac{8\eta{l_2}}{\pi{r_2}^4}V \), \( \cdots \)

If \( P \) be the effective presure difference between the entrance and exit ends of th ecombination, then

\( P=P_1+P_2+\cdots \)

or, \( P=\frac{8\eta{V}}{\pi}\left(\frac{l_1}{{r_1}^4}+ \frac{l_2}{{r_2}^4}+\cdots\right) \)

Therefore,

\( V=\frac{\pi{P}}{8\eta}\frac{1}{ \left(\frac{l_1}{{r_1}^4}+ \frac{l_2}{{r_2}^4}+\cdots\right) } \)

(ii) Flow through capillary tube in parallel combination:

Let us consider a number of capillary tubes of radii \( r_1 \), \( r_2 \), \( r_3 \), \( \cdots \) and length \( l_1 \), \( l_2 \), \( l_3 \), \( \cdots \) respectively are joined in parallel combination.

If \( P \) be the pressure difference maintained across the ends of the combination and \( V_1 \), \( V_2 \), \( \cdots \) be the volume of liquid flowing per second through each tube,then the total volume of liquid following per second is \( V=V_1+V_2+V_3+\cdots \)

Therefore \( V= \frac{\pi{P}{r_1}^4}{8\eta{l_1}} + \frac{\pi{P}{r_2}^4}{8\eta{l_2}}+\cdots \)

or, \( V=\frac{\pi{P}}{8\eta}\left(\frac{{r_1}^4}{l_1}+\frac{{r_2}^4}{l_2}+\cdots\right) \)