Poiseuille’s Formula:
Let us consider, a streamline motion of a liquid through a narrow tube, The streamlines are parallel to the axis of the tube and there is no radial flow of the liquid in the tube. The pressure over any given cross-section normal to the axis of the tube is constant. The pressure varies from point to point along the length of the tube. It is assumed that the liquid in contact with the wall of the tube is at rest.
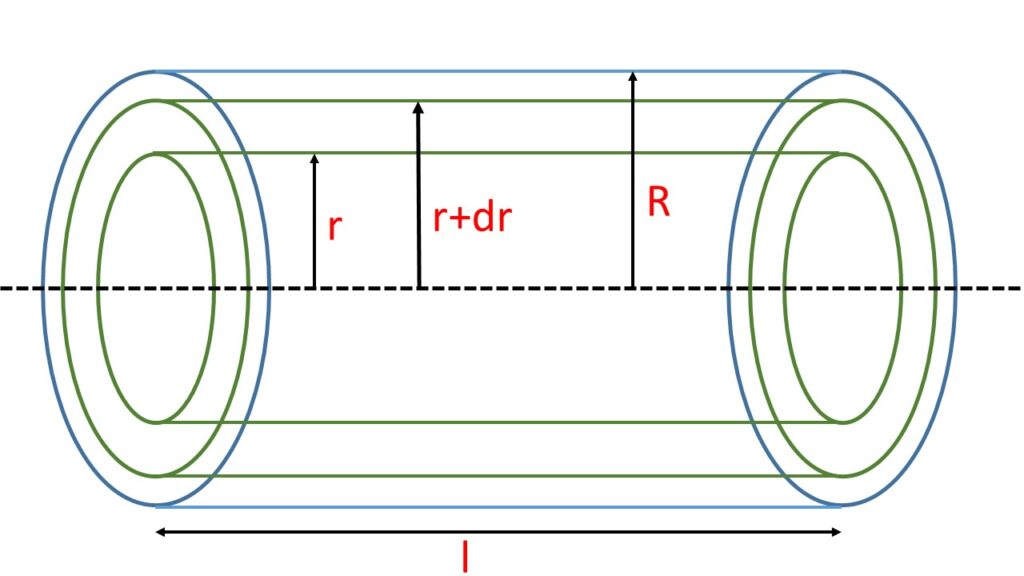
Let us consider a horizontal capillary tube of length l and radius R as shown in the adjoining Fig. 1. Let us also consider that a liquid of coefficient of viscosity \( \eta \) is moving in streamline flow in the tube along the axis of the tube. The velocity of the liquid is maximum along the axis and is zero at the wall of the tube.
Let the velocity at a distance \( r \) from the axis of the tube is \( v \). The velocity gradient is \( \frac{dv}{dr} \) and the viscous drag per unit area is \( \eta\cdot\frac{dv}{dr} \). This force acts over the unit area of the surface of the linear cylinder of the liquid of radius \( r \) in a direction opposite to the pressure gradient. So the total viscous drag or the total resisting force over the whole surface of the liquid cylinder is given by, \( \eta\cdot\frac{dv}{dr}\cdot{2\pi}rl \)
Now if \( P \) be the pressure difference between the ends of the tube, then the force due to the pressure difference tends to accelerate this liquid. this pressure is \( P\cdot\pi{r}^2 \).
At the steady condition,
\( P\pi{r}^2=-\eta\frac{dv}{dr}2\pi{r}l \\or,\ rd=-\frac{2\eta{l}}{P}\,dv \),
where -ve sign indicates that the two types of forces are opposite to each other.
Integrating between the limits r=r to r=R, we get
\( \displaystyle\int_r^R{r\,dr}=-\frac{2l\eta}{P}\displaystyle\int_v^0\,dv \)[here, at \( r=R \), \( v=0 \)]
or, \( \frac{r^2}{2}|_r^R=-\frac{2l\eta}{P}v|_v^0 \)
or, \( \frac{R^2-r^2}{2}=\frac{2l\eta}{P}v \)
or, \( \displaystyle{v=\frac{P}{4l\eta}(R^2-r^2)} \)
This gives the velocity at any distance \( r \) from the axis of the tube.
Now if \( dV \) is the volume of the liquid which flows through the cylindrical shell in unit time between the radii \( r \) and \( r+dr \) then,
\( dV=2\pi{r}\,dr{v} \)or, \( dV=2\pi{r}\,dr \frac{P}{4l\eta}(R^2-r^2) \) ,
So the total volume that passes through the tube in unit time is
\( V=\frac{\pi{P}}{2l\eta}\displaystyle\int_0^R(R^2-r^2)r\,dr \\=\frac{\pi{P}}{2l\eta}[R^2\frac{r^2}{2}-\frac{r^4}{4}]_0^R \)or, \( V= \frac{\pi{P}}{2l\eta}\left(\frac{R^4}{2}-\frac{R^4}{4}\right) \\= \frac{\pi{P}}{2l\eta} \frac{R^4}{4} \)
or, \( \displaystyle{V=\frac{P\pi{R^4}}{8\eta{l}}} \)
This is known as Poiseuille's equation.
