Ans.
Let us consider two particles of masses \( m_1 \) and \( m_2 \) having position vector \( \vec{r_1} \) and \( \vec{r_2} \) with respect to the origin O. Let \( \vec{R} \) be the position vector of centre of mass C with respect to the origin O.
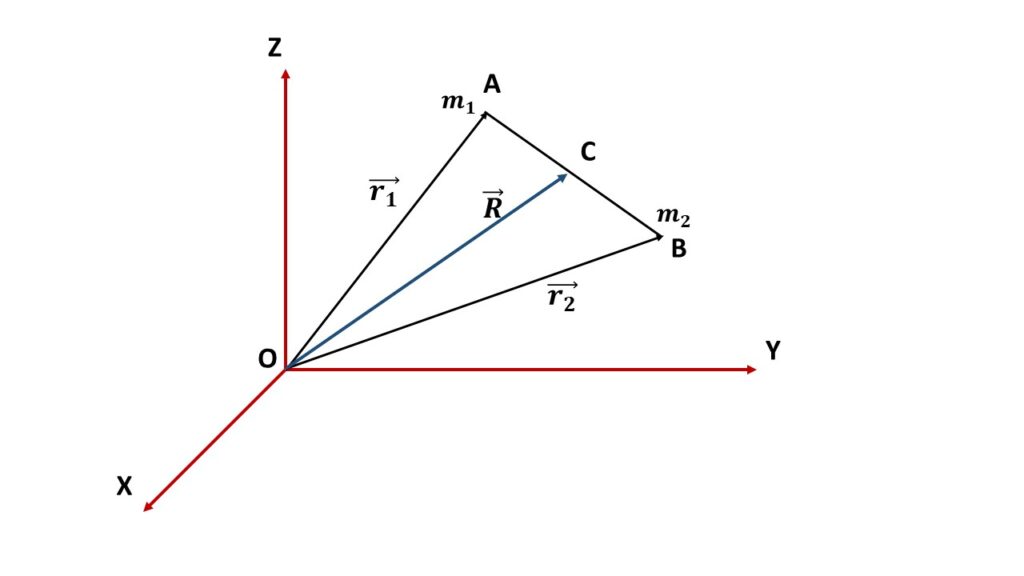
Therefore, \( \displaystyle{\vec{R}=\frac{m_1\vec{r_1}+m_2\vec{r_2}}{m_1+m_2}} \)
or, \( \displaystyle{\dot{\vec{R}}=\frac{m_1\dot{\vec{r_1}}+m_2\dot{\vec{r_2}}}{m_1+m_2}} \)
or, \( \displaystyle{\dot{\vec{R}}=\frac{m_1\vec{v_1}+m_2\vec{v_2}}{m_1+m_2}} \)
or, \( \displaystyle{\vec{V}=\frac{m_1\vec{v_1}+m_2\vec{v_2}}{m_1+m_2}} \)
or, \( (m_1\vec{v_1}+m_2\vec{v_2})=(m_1+m_2)\vec{V}\tag{1} \)
where, \( \vec{v_1} \) and \( \vec{v_2} \) are the velocities of the masses \( m_1 \) and \( m_2 \) respectively and \( \vec{V} \) is the velocity of the centre of mass.
If \( \vec{v} \) be the velocity of \( m_1 \) relative to \( m_2 \) then
\( \vec{v}=\frac{d}{dt}(\vec{r_1}-\vec{r_2})\\=\dot{\vec{r_1}}-\dot{\vec{r_2}} \)
or, \( \vec{v}=\vec{v_1}-\vec{v_2}\tag{2} \)
Solving equations (1) and (2) we get
\( \displaystyle{\vec{v_1}=\vec{V}+\frac{m_2\vec{v}}{m_1+m_2}} \)and, \( \displaystyle{\vec{v_2}=\vec{V}-\frac{m_1\vec{v}}{m_1+m_2}} \)
Therefore the total kinetic energy is given by,
\( T=\frac{1}{2}m_1{v_1}^2+\frac{1}{2}m_2{v_2}^2 \)
\( =\frac{1}{2}m_1{\left(\vec{V}+\frac{m_2\vec{v}}{m_1+m_2}\right)}^2+\frac{1}{2}m_2{\left(\vec{V}-\frac{m_1\vec{v}}{m_1+m_2}\right)}^2 \)
\( =\frac{1}{2}(m_1+m_2)V^2+\frac{1}{2}\frac{m_1m_2}{m_1+m_2}v^2 \)
or, \( T=\frac{1}{2}MV^2+\frac{1}{2}{\mu}v^2 \)
where, \( M=(m_1+m_2) \) is the total mass of the system and \( \mu=\frac{m_1m_2}{m_1+m_2} \) is the reduced mass of the system.