The total moment of mass about the centre of mass:

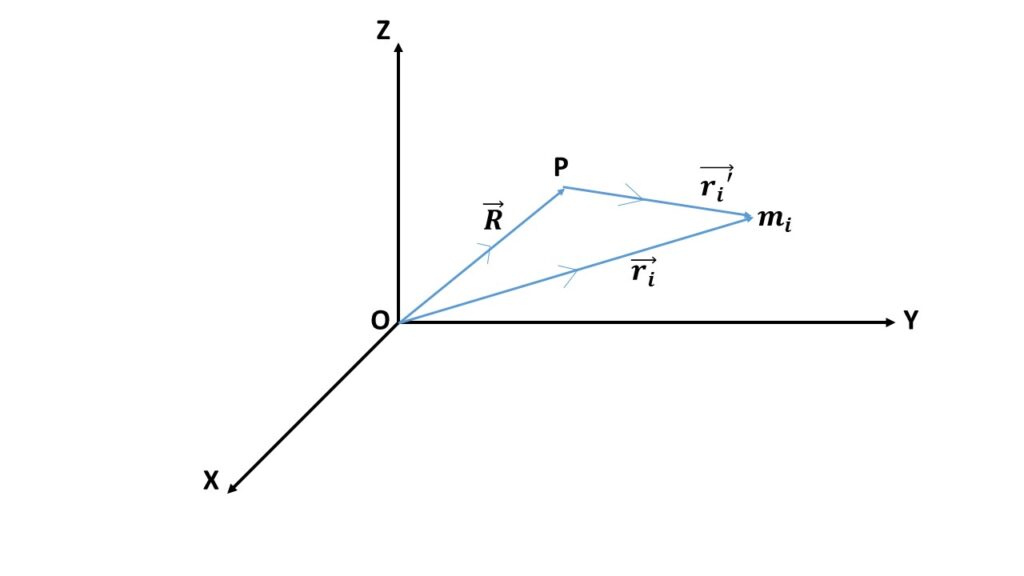
Let us consider a system of n particles of masses \( m_1 \), \( m_2 \), \( \cdots \) \( m_n \) having position vectors \( \vec{r_1} \), \( \vec{r_2} \), \( \cdots \), \( \vec{r_n} \) respectively with respect to the origin O as shown in the above Fig. 1.

Let P be the centre of mass of the system of n particle, with position vector \( \vec{R} \), is given by

\( \displaystyle{\vec{R}=\frac{1}{M}\sum_{i=1}^{n}m_i\vec{r_i}}\tag{1} \)

Where \( \displaystyle{M=\sum_{i=1}^{n}m_i} \) is the total mass of the above system.

Let us consider ith particle of mass \( m_i \) having position vector \( \vec{r_i} \) with respect to the origin \( O \). Let \( \vec{r_i}’ \) be the position vector of the ith particle with respect to the centre of mass point \( P \). So from Fig.1 we can write,

\( \vec{R}+\vec{r_i}’=\vec{r_i}\tag{2} \)

From equations (1) & (2) ,

\( \displaystyle{\vec{R}=\frac{1}{M}\sum_{i=1}^{n}m_i(\vec{R}+\vec{r_i}’)} \)

or, \( M\vec{R}=\displaystyle{\sum_{i=1}^{n}m_i\vec{R}+\sum_{i=1}^{n}m_i\vec{r_i}’} \)

or, \( M\vec{R}=M\vec{R}+\displaystyle{\sum_{i=1}^{n}m_i\vec{r_i}’} \)

or, \( \displaystyle{\sum_{i=1}^{n}m_i\vec{r_i}’}=0\tag{3} \)

So the sum of the products of mass and the position vectors of all the particles about the centre of mass is zero.