(i) Moment of inertia of a solid cone about its axis of symmetry:
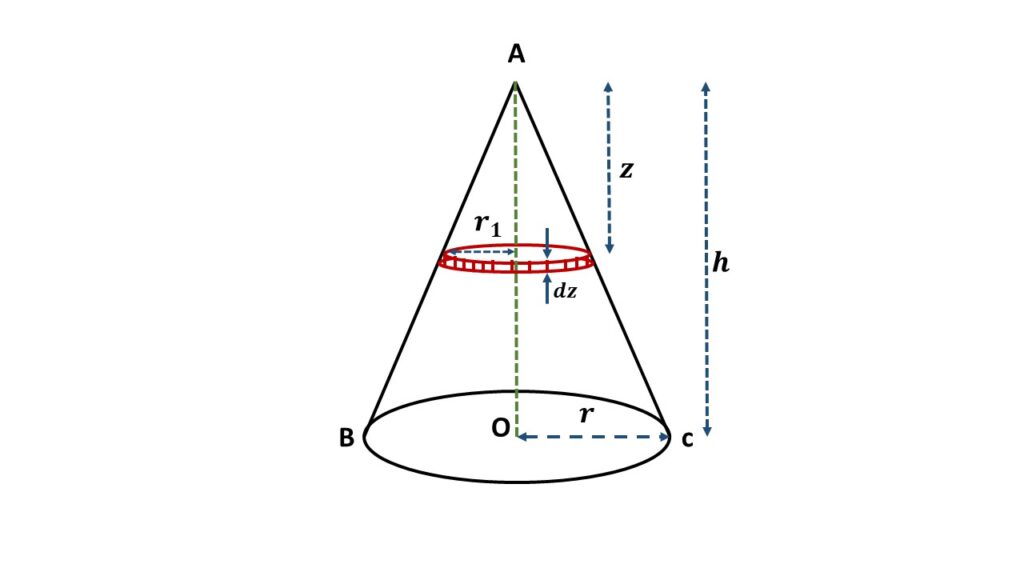
Let us consider a right circular solid cone ABC of mass M and height h, as shown in the above Fig.1. If r be the radius of base of the solid cone then the total volume of this solid cone is \( \frac{1}{3}\pi{r^2}h \).
Mass density i.e., mass per unit volume of the solid cone is \( \sigma=\frac{M}{\frac{1}{3}\pi{r^2}h} \) = \( \frac{3M}{\pi{r^2}h} \).
In order to calculate the moment of inertia of the solid cone about the axis of symmetry AO, let us consider an elementary circular disc of radius \( r_1 \) and thickness \( dz \) at a distance \( z \) from the vertex A. So the volume of this disc is \( (\pi{r_1}^2dz) \) and the mass of this disc is \( \frac{3M}{\pi{r^2}h}\times{\pi{r_1}^2dz} \) = \( \left(\frac{3M{r_1}^2}{r^2{h}}\right)dz \).
From Fig. 1 we can write,
\( \displaystyle{\frac{r_1}{r}=\frac{z}{h}} \)
\( or,\ \displaystyle{r_1=\frac{z}{h}r} \)
So the moment of inertia of the elementray disc about the axis of symmetry is
\( dI=\frac{1}{2}\left(\frac{3M{r_1}^2}{r^2{h}}\right)dz\times{r_1}^2 \)
[ To read the full derivationn of moment of inertia of a solid circilar disc about a axis passing through the centre of mass of it and perpendicular to the plane of it, (CLICK HERE) ]
\( or,\ dI=\displaystyle{\frac{3M}{2{r^2}h}{r_1}^4\ dz} \)
\( or,\ dI=\displaystyle{\frac{3M}{2{r^2}h}\frac{z^4r^4}{h^4}\ dz} \)
[putting the value of \( r_1 \)]
\( or,\ dI=\displaystyle{\frac{3Mr^2}{2h^5}z^4\ dz} \)
So the moment of inertia of the whole solid cone about the axis of symmetry AO is
\( I=\displaystyle{\frac{3Mr^2}{2h^5}\int_0^h{z^4}\ dz} \)
\( or,\ I=\displaystyle{\frac{3Mr^2}{2h^5}\frac{1}{5}\left[{z^5}\right]_0^h} \)
\( or,\ I=\displaystyle{\frac{3Mr^2}{10h^5}h^5} \)
\( or,\ \displaystyle{I=\frac{3}{10}Mr^2} \)
(ii) Moment of inertia of a solid cone about the axis passing through the vortex and perpendicular to the axis of symmetry:
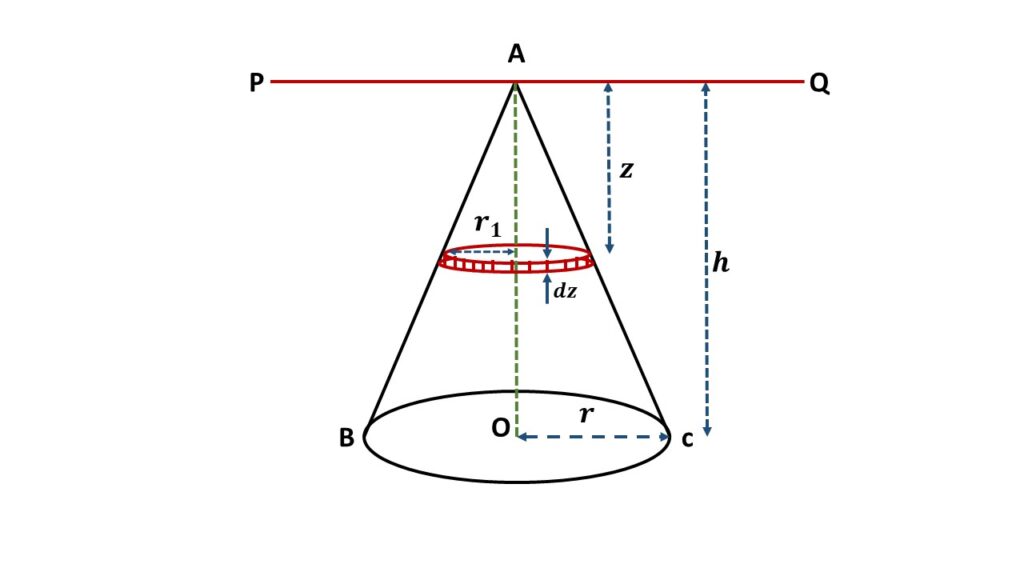
Let us consider a right circular solid cone ABC of mass M and height h, as shown in the above Fig.2. If r be the radius of base of the solid cone then the total volume of this solid cone is \( \frac{1}{3}\pi{r^2}h \).
Mass density i.e., mass per unit volume of the solid cone is \( \sigma=\frac{M}{\frac{1}{3}\pi{r^2}h} \) = \( \frac{3M}{\pi{r^2}h} \).
Let us consider an axis PQ passing through the vortex \( A \) and perpendicular to the axis of symmetry \( AO \).
In order to calculate the moment of inertia of the solid cone about the axis PQ, let us consider an elementary solid circular disc of radius \( r_1 \), thickness \( dz \) at a distance \( z \) from the vortex \( A \).
From Fig. 2 we can write
\( \displaystyle{\frac{r_1}{r}=\frac{z}{h}} \)
\( or,\ \displaystyle{r_1=\frac{z}{h}r} \)
The volume of this disc is \( (\pi{r_1}^2dz) \) and the mass of this disc is \( \frac{3M}{\pi{r^2}h}\times{\pi{r_1}^2dz} \) = \( \left(\frac{3M{r_1}^2}{r^2{h}}\right)dz \)
So the moment of inertia of the disc about its diameter parallel to the axis PQ is,
\( I_d=\frac{1}{4}\times(mass\ of\ the\ disc)\times{r_1}^2 \)
\( or,\ I_d=\displaystyle{\frac{3M}{4r^2h}{r_1}^4\ dz} \)
\( or,\ I_d=\displaystyle{\frac{3Mr^2}{4h^5}{z}^4\ dz} \)
[putting the value of \( r_1 \)]
So by applying the theorem of parallel axes we can write that the moment of inertia of the elementary disc about the axis PQ is given by,
\( dI_{PQ}=I_d+\left(\frac{3M{r_1}^2}{r^2{h}}\right)dz\times{z^2} \)
\( or,\ dI_{PQ}=I_d+\frac{3M}{h^3}z^4\ dz \)
[putting the value of \( r_1 \)]
\( or,\ dI_{PQ}=\displaystyle{\frac{3Mr^2}{4h^5}{z}^4\ dz}+\displaystyle{\frac{3M}{h^3}z^4\ dz} \)
So the moment of inertia of the solid cone about the axis \( PQ \) is given by,
\( I_{PQ}=\frac{3Mr^2}{4h^5}\displaystyle{\int_0^h}z^4\ dz+\frac{3M}{h^3}\displaystyle{\int_0^h}z^4\ dz \)
\( or,\ I_{PQ}=\frac{3Mr^2}{4h^5}\frac{h^5}{5}+\frac{3M}{h^3}\frac{h^5}{5} \)
\( or,\ I_{PQ}=\frac{3Mr^2}{20}+\frac{3Mh^2}{5} \)
\( or,\ \displaystyle{I_{PQ}=\frac{3M}{5}\left(\frac{r^2}{4}+h^2\right)} \)