(i) Moment of inertia of a triangular lamina about one of its side:

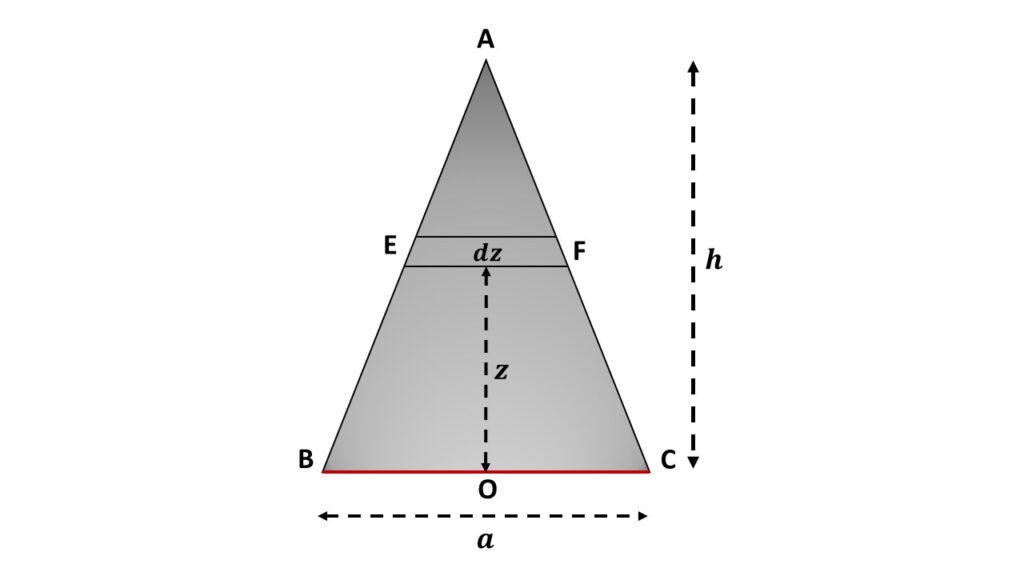
Let us consider a triangular lamina ABC of mass M, is rotating about one of its sides BC, where the length of the side BC is a. If \( h \) be the height of this lamina, then the area of this lamina is \( \left(\frac{1}{2}\cdot{a}\cdot{h}\right) \) and the mass density i.e., mass per unit area is \( \frac{M}{\frac{1}{2}ah} \) = \( \left(\frac{2M}{ah}\right) \).

In order to calculate the moment of inertia of this lamina about the axis of rotation BC, let us consider a small elementary area \( EF \) of thickness \( dz \) and length \( l \) at a distance \( z \) from the axis of rotation BC. So the area of \( EF \) is \( l\cdot{dz} \) and the mass is \( \left(\frac{2M}{ah}\right)l\ dz \). Now the moment of inertia of this element about the axis of rotation is

\( dI=\left(\frac{2Ml}{ah}\right)z^2\ dz\tag{1} \)

From Fig. 1, we can write that

\( \left(\frac{l}{h-z}\right)=\left(\frac{a}{h}\right) \)

\( or,\ \displaystyle{l=\frac{a(h-z)}{h}} \)

Putting the value of \( l \) in equation (1) we get,

\( dI=\left(\frac{2M}{ah}\right)\frac{a(h-z)}{h}z^2\ dz \)

\( or,\ dI=\frac{2M}{h^2}(h-z)z^2\ dz \)

So the moment of inertia of the whole triangular lamina is

\( I=\frac{2M}{h^2}\displaystyle{\int_0^h}(h-z)z^2\ dz \)

\( or,\ I=\frac{2M}{h^2}\displaystyle{\int_0^h}(hz^2-z^3)\ dz \)

\( or,\ I=\frac{2M}{h^2}{\left[\frac{1}{3}hz^3-\frac{1}{4}z^4\right]}_0^h \)

\( or,\ I=\frac{2M}{h^2}{\left[\frac{1}{3}h^4-\frac{1}{4}h^4\right]} \)

\( or,\ I=\frac{2M}{h^2}\frac{1}{12}h^4 \)

\( or,\ \displaystyle{I=\frac{1}{6}Mh^2}\tag{2} \)

(ii) About an axis passing through the centre of gravity and parallel to one side of the triangular lamina:

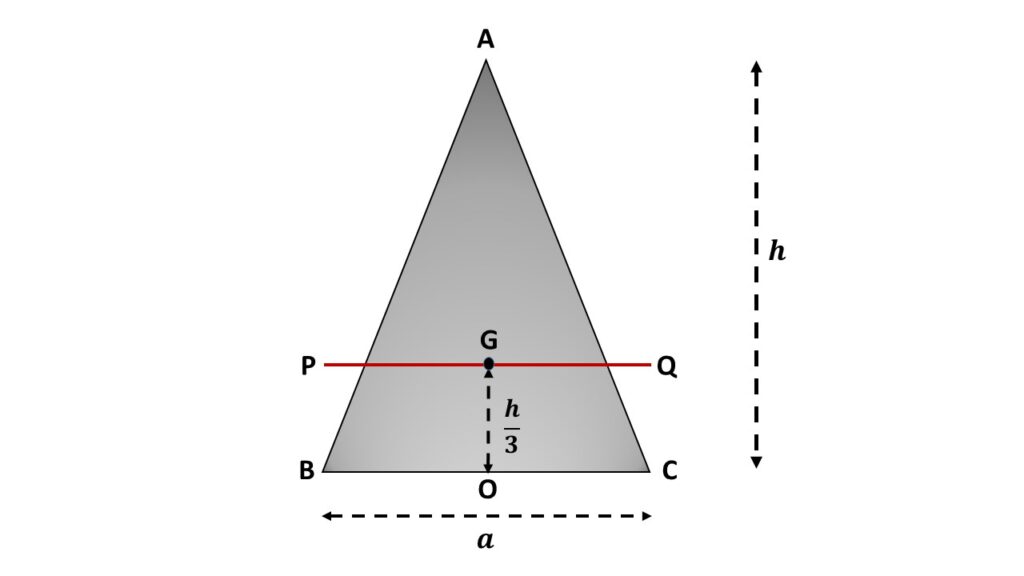
Let us consider the rectangular lamina ABC is rotating about an axis PQ passing through the centre of gravity G of the lamina and parallel to the side BC. We know that the perpendicular distance of G from each side is \( \left(\frac{h}{3}\right) \), where h is the height of the triangular lamina.

So the perpendicular distance between PQ and BC is \( (\frac{h}{3}) \)

If \( I_G \) be the moment of inertia of this lamina about the axis PQ, then by applying the theorem of parallel axes, we can write that

\( I=I_G+M{\left(\frac{h}{3}\right)}^2 \)

\( or,\ I_G=I-\frac{1}{9}Mh^2 \)

\( or,\ I_G=\frac{1}{6}Mh^2-\frac{1}{9}Mh^2 \)
[putting the value of \( I \) from equation (2)]

\( or,\ \displaystyle{I_G=\frac{1}{18}Mh^2}\tag{3} \)

(iii) Moment of inertia of the rectangular lamina about an axis passing through one of its vertices and parallel to opposite side:

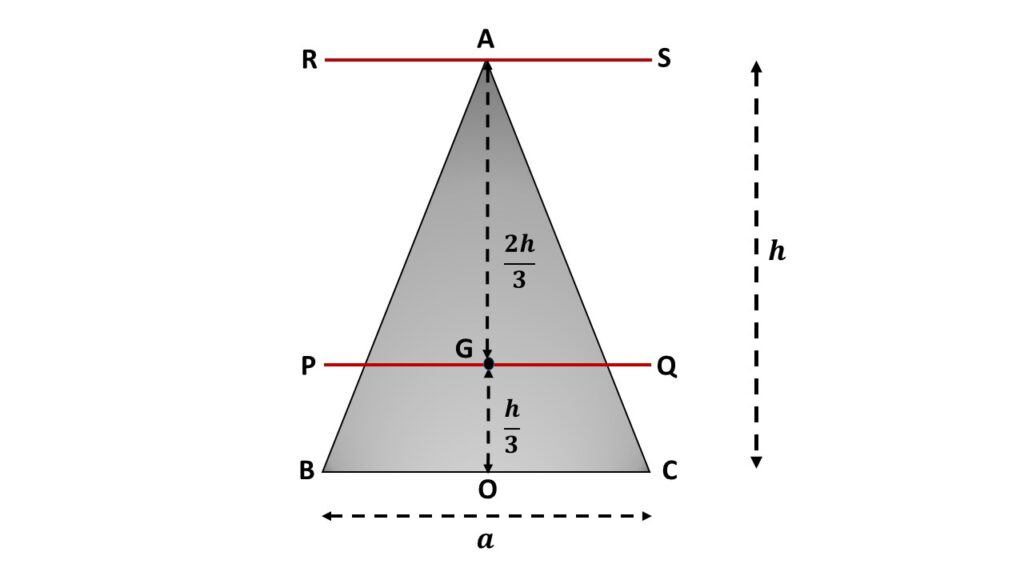
Let us consider the rectangular lamina ABC is rotating about an axis RS passing through vertex A and parallel to the side BC. We know that the distance of each vertex from the centre of gravity is \( \left(\frac{2h}{3}\right) \), where h is the height of the rectangular lamina. So the perpendicular distance between PQ and RS is \( \left(\frac{2h}{3}\right) \).

By applying the theorem of parallel axes, we can write that the moment of inertia of this rectangular lamina about the axis of rotation \( RS \) is

\( I_V=I_G+M{\left(\frac{2h}{3}\right)}^2 \)

\( or,\ I_V=\frac{1}{18}Mh^2+\frac{4}{9}h^2 \)
[putting the value of \( I_G \) from equation (3)]

\( or,\ \displaystyle{I_V=\frac{1}{2}Mh^2}\tag{4} \)