Transverse vibration of a loaded cantilever:
Let us consider a light cantilever MN of length l is clamped horizontally at one and M and is loaded by a weight W at the other end N, the weight W acts in the vertically downward direction. If \( m \) be the mass of the weight \( W \), then \( W=mg \), where g is the acceleration due to gravity. We know that the depression of this free end is
\( \displaystyle{y=\frac{Wl^3}{3YAK^2}}\tag{1} \)
[Read In Detail]
where Y is Young’s modulus of the material of the beam, A is the cross-sectional area and K is the radius of gyration of the beam.
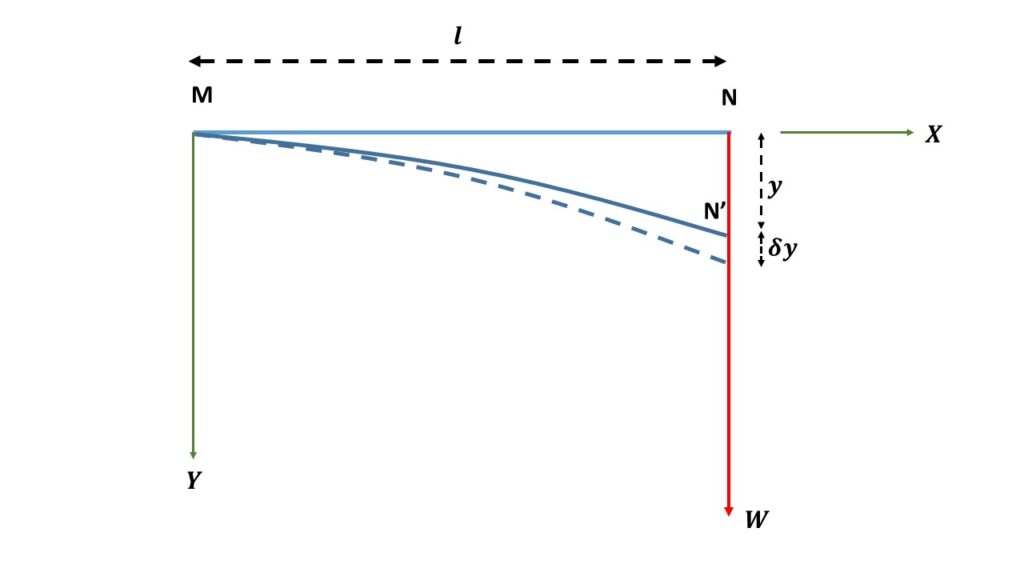
Now the beam is depressed further through a small distance \( \delta{y} \) by applying a force \( F \) at the free end.
Then \( \displaystyle{y+\delta{y}=\frac{(W+F)l^3}{3YAK^2}}\tag{2} \)
From equations (1) and (2) we get,
\( \displaystyle{\delta{y}=\frac{Fl^3}{3YAK^2}} \)
or, \( \displaystyle{F=\frac{3YAK^2}{l^3}\delta{y}} \)
There is a motion of the weight in the upward direction by the elastic force \( -F \), as soon as the depressing force \( F \) is removed.( Since the positive direction of Y-axis is taken here vertically downward.)
So the equation of motion of the load of mass \( m \) is
\( \displaystyle{m\frac{d^2\delta{y}}{dt^2}=-F} \)
or, \( \displaystyle{m\frac{d^2\delta{y}}{dt^2}=-\frac{3YAK^2}{l^3}\delta{y}} \)
or, \( \displaystyle{\frac{d^2\delta{y}}{dt^2}+\frac{3YAK^2}{ml^3}\delta{y}=0} \)
or, \( \displaystyle{\frac{d^2\delta{y}}{dt^2}+{\omega}^2{\delta{y}}=0} \)
Here, \( {\omega}^2=\frac{3YAK^2}{ml^3} \)
This is the equation of simple harmonic motion about the equilibrium position. So the time period is given by,
\( \displaystyle{T=\frac{2\pi}{\omega}\\=\frac{2\pi}{\sqrt{\frac{3YAK^2}{ml^3}}}\\=2\pi\sqrt{\frac{ml^3}{3YAK^2}}} \)
\( \displaystyle{T=2\pi\sqrt{\frac{Wl^3}{3YAK^2{g}}}} \)