Depression of a beam supported at the ends:
Let us consider a uniform rectangular beam of negligible weight supported at the two knife edges at the points M and N in the same horizontal plane, as shown in the adjoining figure.
A weight \( W \) is applied at the middle point \( O \) of the beam. So the reaction at each knife-edge is \( \frac{W}{2} \) in the vertical upward direction.
Since the middle part of the beam is horizontal, the beam may be considered as equivalent to two inverted cantilevers. Each of these two cantilevers is fixed at the point \( O \) and a load \( \frac{W}{2} \) is applied at other ends M and N, as a result, a bending is produced in the vertically upward direction.
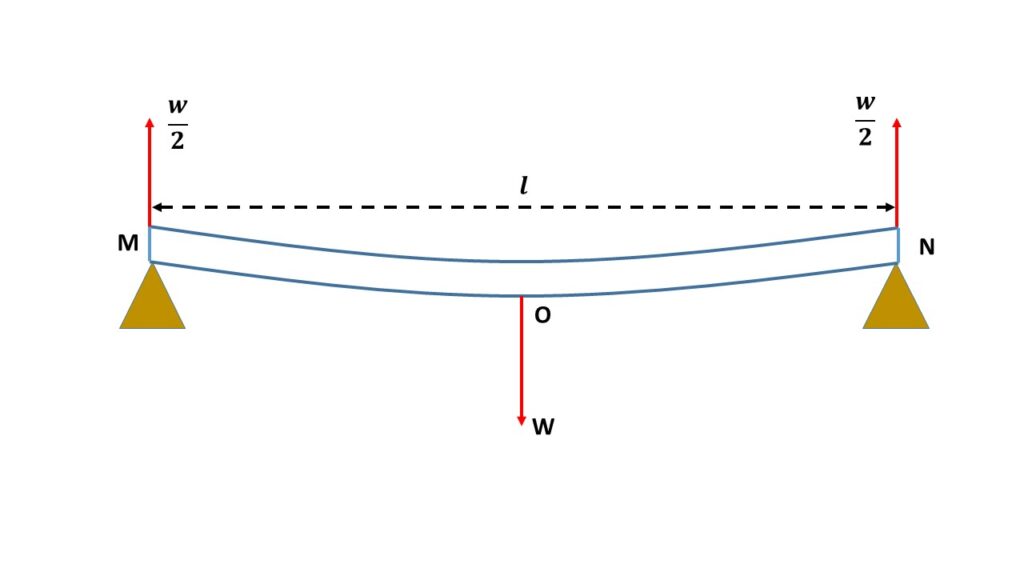
If the length of the rectangular beam is \( l \) then the length of each cantilever is \( \frac{l}{2} \). Now the elevation of M and N above the mid point \( O \) is
\( \displaystyle{y=\frac{\frac{W}{2}\cdot{(\frac{l}{2})}^3}{3YI}\\=\frac{Wl^3}{48YI}} \)
[Read In Detail]
where, \( I \) is the geometrical moment of inertia and \( Y \) is Young’s modulus of the materal of the beam.
Since the beam has a rectangular cross sectional area of breadth \( b \) and depth \( d \), then the geometrical moment of inertia \( \displaystyle{I=\frac{bd^3}{12}} \)
Therefore, \( \displaystyle{y=\frac{Wl^3}{48Y}\frac{12}{bd^3}\\=\frac{Wl^3}{4Ybd^3}} \)