Work:

When a force acting on a body, physically displaces the body through a distance in the direction of the force, then it is said that work is done by the force.

So the work depends on two factors:

• The force acting on the body
• The displacement of the body along the direction of the force

Work done by a constant force:

The work done by a force is measured by the product of the force acting on the body and the displacement of the body along the direction of the force.

Let us consider the force \( \vec{F} \) be the force acting on a abody at an angle \( \theta \) with the direction of the displacement \( \vec{S} \) of the body, as shown in Fig.1

So the work done in this case is given by,

\( W=\vec{F}\cdot\vec{S}=FS\ \cos\theta\tag{1} \)

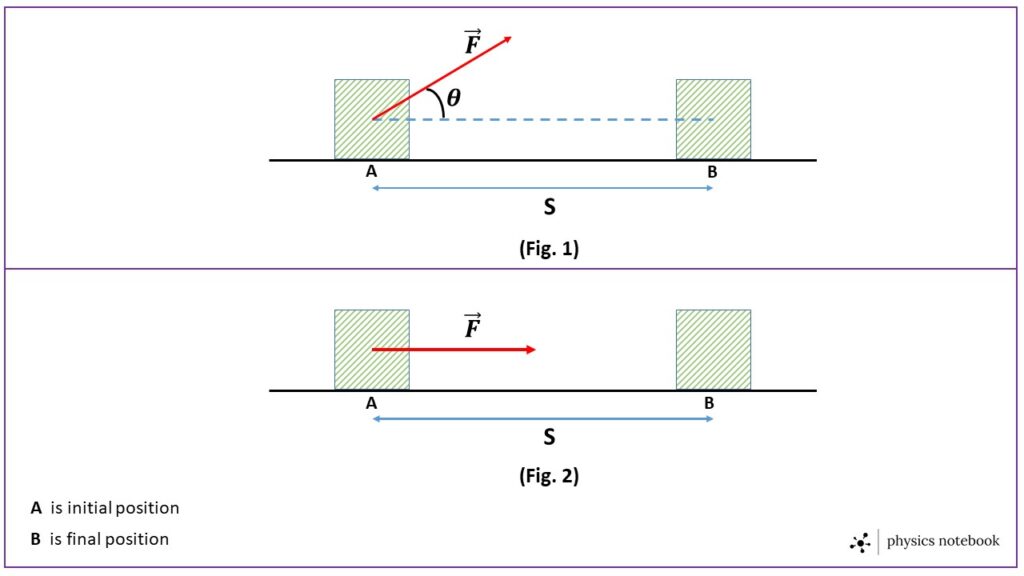
Let us consider \( \vec{F} \) be the force acting on a body and \( \vec{S} \) be the displacement of the body along the direction of the force, as shown in the Fig.2.

So the work done by the force is given by,

\( W=\vec{F}\cdot{\vec{S}} \)

\( or,\ W=FS\ \cos\theta=FS\tag{2} \)

where, \( \theta \) is the angle between force \( \vec{F} \) and displacement \( \vec{S} \), in this case, since the body is displaced in the direction of the force, so  \( \theta=0 \) and \( \cos\theta=1 \)

Since the work done is the scaler product of two vector quantities (force and displacement), therefore work done is the scalar quantity. It only has magnitude, no direction.

From equation (1), we can surely say that there are thee conditions, when the work done will be zero:

1. When the displacement is zero, i.e. there will be no displacement of the body after the application of force on the body, in this case no work is done by the acting force.
   For example: when you push a wall, the wall does not move, so in this situation, the work done by you is zero.
2. The force acting on the body is zero, then the work done is zero.
3. If the force acting on a body and the displacement of that body are mutually perpendicular to each other, then the work done by the body will be zero.
4. in this case, \( \theta=90^{\circ} \), then  \( W=FS\ \cos{90}^{\circ}=0 \).
   For example: Centripetal force in a uniform circular motion of a particle and the velocity of the particle are perpendicular to each other, for this reason, centripetal force does not do any work on the particle.

Dimension of work is [Force]\( \times \)[Displacement]= \( [ML{T}^{-2}]\times[L] \)= \( [ML^2T^{-2}] \)

Unit of work is Joule (S.I. unit) and Erg. (C.G.S. unit)

If a force of one Newton displaces the body through a distance of one meter along the direction of the acting force then the work done by the force is said to be one Joule.

Relation between Joule and Erg is, \( 1\ Joule=10^7\ Ergs \)

Work done by a variable force:

There are so many situations, where the body moves under the effect of variable force. For example, the gravitational force acting on a freely falling body. Because we know that in case of the gravitational force, the force varies inversely with the square of the distance.

Let us consider \( \vec{F} \) be the force acting on a particle, and \( d\vec{r} \) be the displacement of the particle under the effect of the force.

Then the work done by the force on the particle is given by,

\( dW=\vec{F}\cdot{d}\vec{r} \)

since only the component of \( \vec{F} \)in the direction of \( d\vec{r} \) is responsible for the motion of the particle.

So the work done by the force \( \vec{F} \) in moving the particle from the initial position A to the final position B along the curve C is given by,

\( \displaystyle{W=\int_{C}\left(\vec{F}\cdot{d}\vec{r}\right)} \)

Let, \( \vec{r_1} \) and \( \vec{r_2} \) be the position vectors of the points A and B respectively with respect to the origin O, then we can write,

\( \displaystyle{W=\int_{A}^{B}\left(\vec{F}\cdot{d}\vec{r}\right)} \)

\( or,\ \displaystyle{W=\int_{{r_1}}^{{r_2}}\left(\vec{F}\cdot{d}\vec{r}\right)} \)