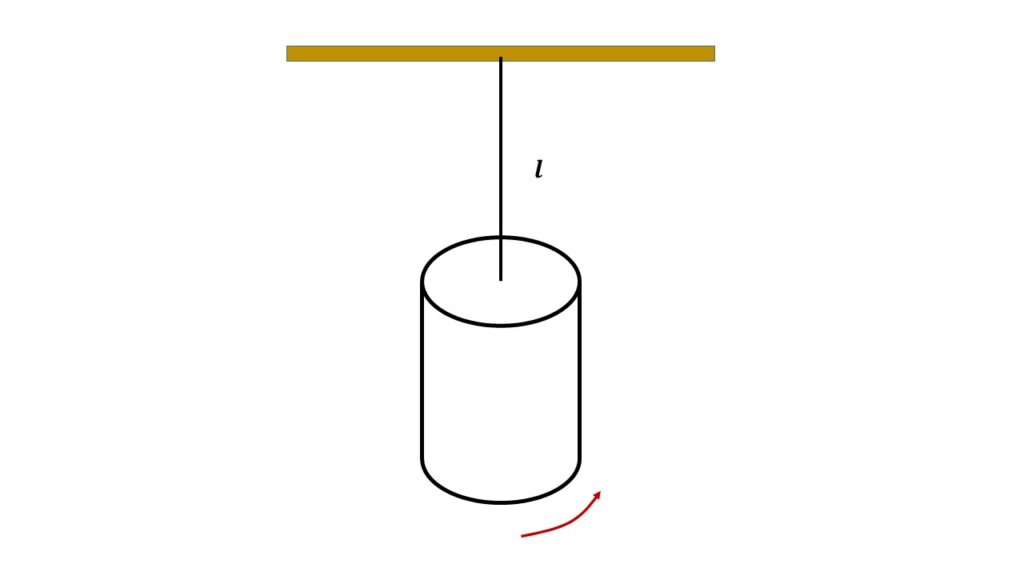
Torsional Pendulum:
A heavy cylindrical rod or disc is suspended from one end of a fine wire which is attached to its centre and the upper end is fixed. This system constitutes a torsional pendulum.
The cylindrical rod or disc is twisted in a plane perpendicular to the axis of the cylindrical rod, as a result, there is a twist in the wire. When the cylindrical rod is released, it executes a torsional vibration about the wire as an axis.
Let, the wire be twisted through an angle \( \theta \) and a restoring couple is set up within the wire. This restoring couple is given by, \( \frac{\pi\eta{r^4}}{2l}\theta \).
Where, \( l \)=length of the wire, \( r \)=radius of the wire, \( \eta \)= modulus of rigidity of the material of the wire.
Let, \( I \) be the moment of inertia of the cylindrical rod or disc about the wire.
Then the deflecting couple is \( I\cdot\frac{d^2{\theta}}{d{t}^2} \), where \( \frac{d^2\theta}{d{t}^2} \) is the angular acceleration of the cylindrical rod or disc.
In equilibrium condition,
\( \displaystyle{I\frac{d^2{\theta}}{dt^2}=-\frac{\pi\eta{r^4}}{2l}\theta\\or,\ I\frac{d^2\theta}{dt^2}+\frac{\pi\eta{r}^4}{2l}\theta =0\\or,\ I\ddot{\theta}+\tau\theta=0\\or,\ \ddot{\theta}+\frac{\tau}{I}\theta\\or,\ \ddot{\theta}+{\omega}^2\theta=0 }\)
This the equation of simple harmonic motion.
where, \( \tau=\frac{\pi\eta{r^4}}{2l} \) is the torsional rigidity i.e., twisting couple per unit twist,
\( \omega \) is the angular velocity,
\( {\omega}^2=\frac{\tau}{I}=\frac{\pi\eta{r^4}}{2lI} \),
If \( T \) be the time period then \( T=\frac{2\pi}{\omega} \).
Now, \( \displaystyle{T=\frac{2\pi}{\omega}=\frac{2\pi}{\sqrt{\frac{\tau}{I}}}=2\pi\sqrt{\frac{I}{\tau}}} \)
The modulus of rigidity is given by,
\( \displaystyle{\eta=\frac{2lI{\omega}^2}{\pi{r}^4}\\=\frac{2LI4{\pi}^2}{\pi{r}^4{T}^2}\\=\frac{8\pi{lI}}{T^2{r}^4}} \)