Time period of an artificial satellite:

Let us consider an artificial satellite revolves around the earth with a velocity \( v \), at a height \( h \) from the surface of the earth. Mass of the earth is \( M \) and radius is \( R \).

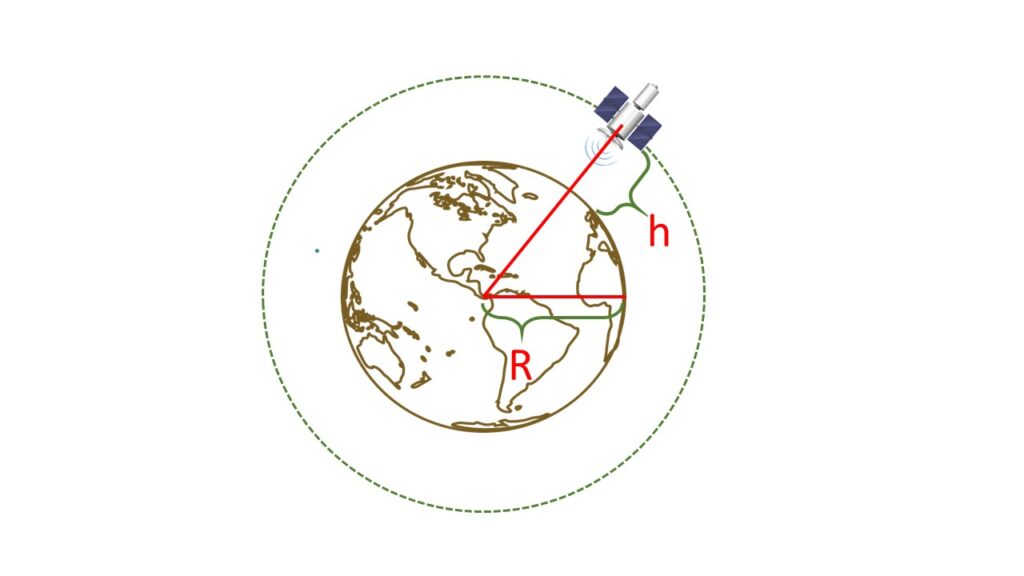
Here, the gravitational force of attraction is equal to centrifugal force on the satellite.

\( \frac{GMm}{{(R+h)}^2}=\frac{mv^2}{(R+h)} \\or,\ v=\sqrt{\frac{GM}{R+h}} \)

where \( G \) is the gravitational constant.

Now the time period of the satellite is,

\( T=\frac{2\pi(R+h)}{v} \\=\frac{2\pi(R+h)}{\sqrt{\frac{GM}{R+h}}} \\=2\pi(R+h)\sqrt{\frac{R+h}{GM}} \)

We know that the acceleration due to gravity \( g=\frac{GM}{R^2} \),

\( T=2\pi(R+h)\frac{\sqrt{R+h}}{gR^2} \)

or, \( \displaystyle{T=2\pi\frac{(R+h)}{R}\sqrt{\frac{R+h}{g}}} \)