Equation of Continuity:
When a fluid ( liquid or gas ) flows in a tube of flow in streamline motion, the rate of flow of mass of the fluid through any cross-sectional area of the tube remains the same, this means that the quantity of fluid entering one end of a flow per second is the same as leaving the tube at the other end of a flow tube per second. It is known as the equation of continuity.
Let us consider two sections of a flow tube at the points \( A \) and \( B \) having cross-sectional areas \( \alpha_1 \) and \( \alpha_2 \) respectively, let \( v_1 \) and \( v_2 \) be the velocities at A and B respectively, \( \rho_1 \) and \( \rho_2 \) be the densities of the fluid at \( A \) and \( B \) respectively.
The mass of fluid crossing the cross-section \( \alpha_1 \) per second is \( v_1\alpha_1\rho_1 \) and the mass of fluid crossing the cross-section \( \alpha_2 \) per second is \( v_2\alpha_2\rho_2 \)
Since there are no sources or sinks with the volume between the sections A and B, by using the law of conservation of matter we can write
\( v_1\alpha_1\rho_1=v_2\alpha_2\rho_2 \)Since the fluid is incompressibe, therefore \( \rho_1=\rho_2 \)
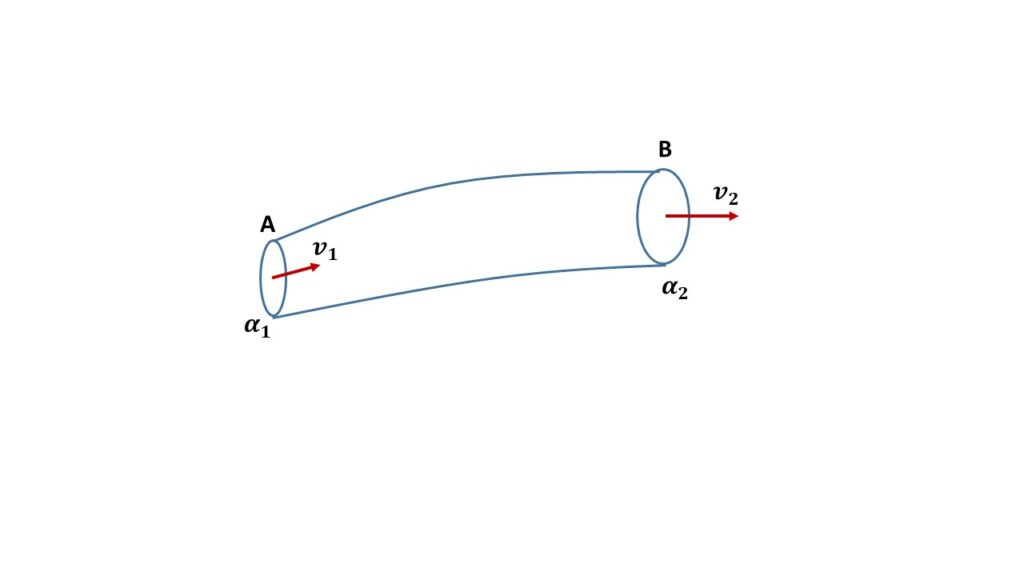
Now we can write, \( v_1\alpha_1=v_2\alpha_2 \)
therefore, \( \displaystyle{v\alpha=constant} \)
This the mathematical expression of equation of continuity.