Surface Energy:
Due to the surface tension of the liquid, the surface of the liquid tends to decrease the surface area. Hence when the area of a liquid surface is increased, work is done against the surface tension. This work is stored on the surface of the liquid and it is known as the surface energy.
Relation Between Surface Tension and Surface Energy:
Let us consider a liquid film is produced in a rectangular wire \( MNOP \). Now the side \( MN \) of that rectangular film is movable and can be shifted along \( PM \) and ON. If T be the surface tension of the liquid and l be the length of \( MN \), then the inward attractive force due to the surface tension on the side \( MN \) is \( 2T\times{l} \). Here the factor 2 appears, since the film has two surfaces. So to keep MN in position, a force has to be applied in the outward direction. This outward force must be equal and opposite to that of the inward force due to surface tension. So at equilibrium \( F=2Tl \).
Now the wire \( MN \) is pulled in an outward direction through a small distance dx into the position \( M’N’ \), keeping the temperature constant throughout this process. So the work done is
\( F\times{dx}=2Tldx \)Here the increase in surface area is \( 2ldx \) [the factor 2 appears since the film has two surfaces.]
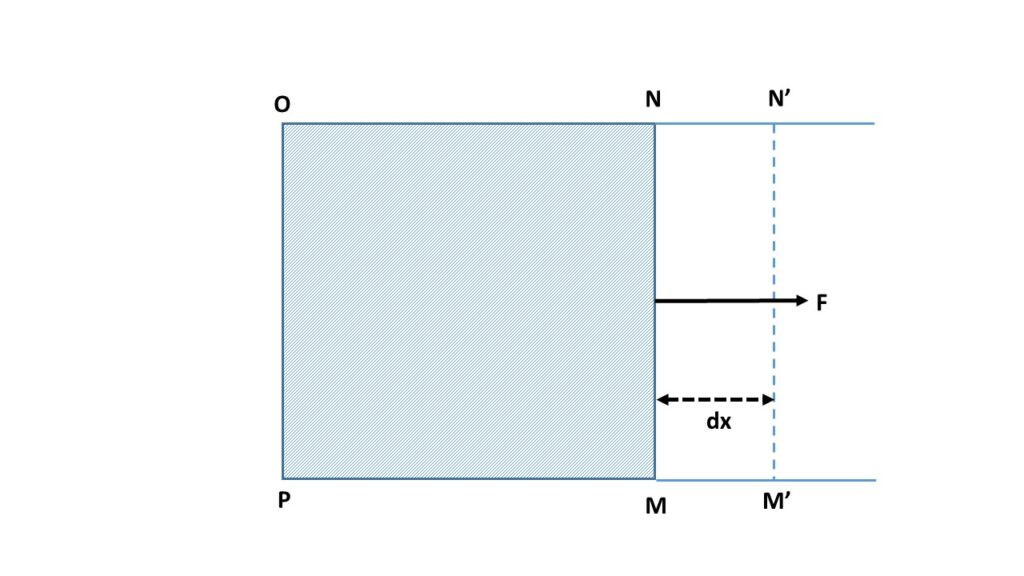
This work done is stored in the liquid surface as surface energy. So the surface energy per unit area is numerically equal to the surface tension.
Actually, when the film is stretched, it gets cooled and therefore absorbs heat from the atmosphere to keep the temperature constant. If \( h \) be the amount of heat absorbed per unit area to maintain the temperature constant, so the total surface energy of new surface area \( 2ldx \) is given by,
\( E\times{2ldx}=T\times{2ldx}+h\times{2ldx} \)or, \( E=T+h \tag{1} \)
Where \( E \) is the surface energy per unit area.
Here the surface energy consists of two parts (i) mechanical energy [ \( T \)] and (ii) thermal energy[ \( h \)]. The mechanical part of the surface energy of a liquid film is free energy. so we can write the surface energy of the liquid is equal to the free energy of the liquid film.
The dimension of surface energy is \( \frac{ML^2T^{-2}}{L^2}=MT^{-2} \)
If \( \theta \) is the temperature in absolute scale and \( \frac{dT}{d\theta} \) is the temperature coefficient of surface tension, then \( h=-\theta\frac{dT}{d\theta} \).
Now equation (1) can be written as, \( E=T-\theta\frac{dT}{d\theta} \tag{2} \)
At absolute zero temperature \( \theta=0 \), and when surface tension does not change with temperature [ \( \frac{dT}{d\theta}=0 \)] then equation (2) becomes, \( E=T \).
In case of almost all liquid surface tension decreases with the rise of temperature, this means that \( \frac{dT}{d\theta} \) is negative. Now equation (2) becomes
\( E=T+\theta\frac{dT}{d\theta} \), i.e., \( E>T \)