Gravitational Constant (G):

If \( m_1 \) and \( m_2 \) are the two masses of two bodies respectively separated by a distance r, the force of attraction F along the line joining the centres of the two bodies is

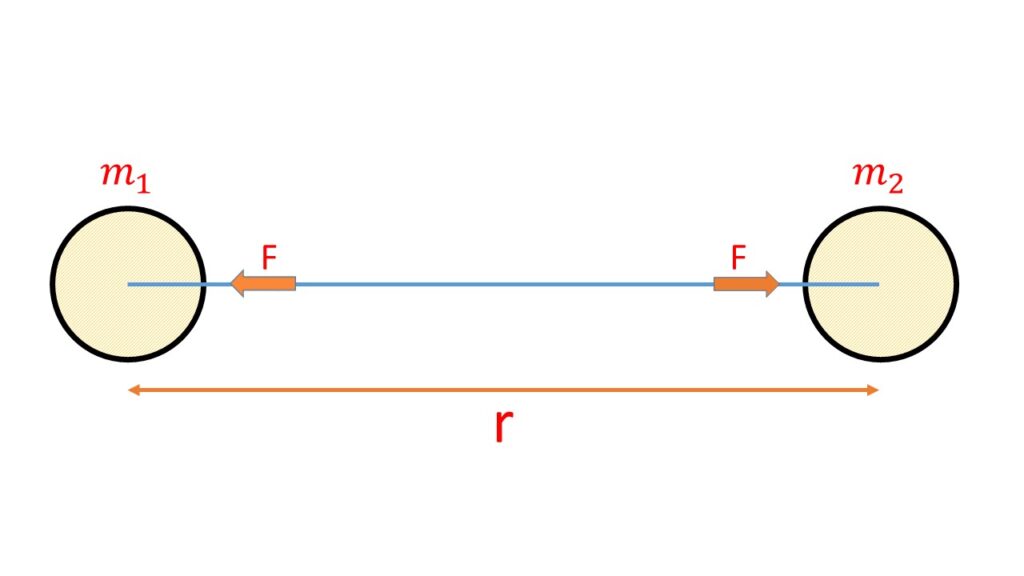
F \alpha \frac{m_1 m_2}{r^2}

F = G \frac{m_1m_2}{r^2}

Where G is the constant of proportionality and is called the Gravitational Constant.

If \( m_1= m_2= 1 \) and \( r=1 \) then \( F=G \). Therefore the gravitational constant is equal to the force of attraction between two bodies each of unit mass separated by a unit distance apart.

Dimension of G:

F = G \frac{m_1m_2}{r^2}

G=\frac{Fr^2}{m_1m_2}

Dimension of G is \( \frac{MLT^{-2}L^2}{M^2} \) = \( M^{-1}L^3T^{-2} \)

Units of G:

The units of G are

• dyne cm² /gm² in c.g.s. unit,
• poundal-ft²/lb² in F.P.S. unit,
• newton-mt²/kg² in S.I. unit.

Magnitude of G:

The vale of G is 6.670 * 10^-8 dyne-cm²/gm² and 6.670 * 10^-11 newton-mt²/kg² .