Escape Velocity:
Escape velocity is defined as the minimum velocity with which an object is projected from the surface of a planet so that the object does not come back to the surface of the planet.
Escape velocity does not depend upon the mass of the projected object.
Escape velocity depends upon the radius of the planet.
Expression of Escape Velocity:
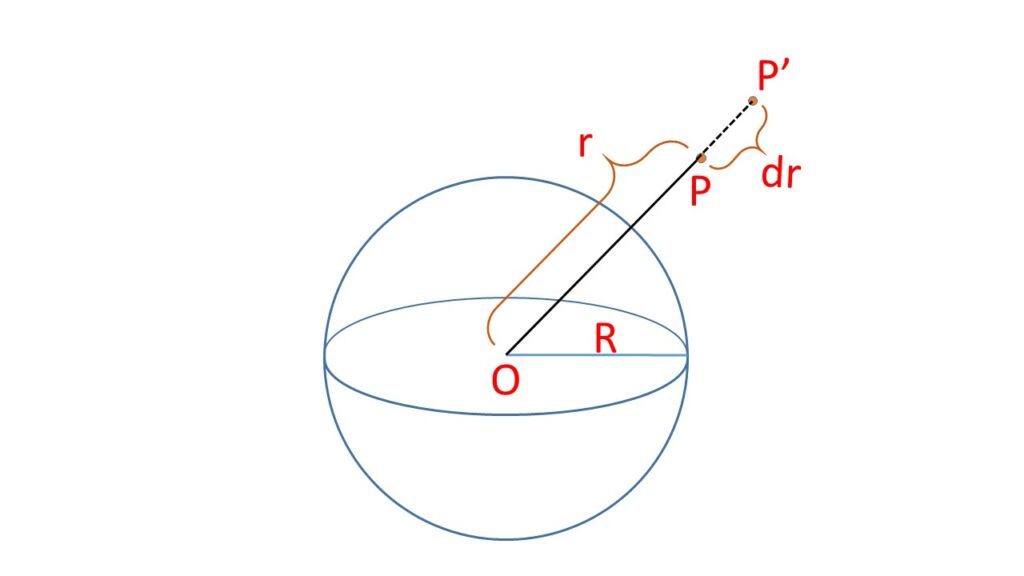
Let us consider the mass of the earth is \( M \) and the radius is \( R \). A body of mass \( m \) is situated at the point \( P \) at a distance \( r \) from the centre of the earth \( O \), as shown in the adjoining Fig.1, where \( r>R \).
Now the force with which the body is attracted by the earth, toward its centre is given by,
\( F=G\frac{Mm}{r^2} \) where \( G \) is the gravitational constant.
Now the body of mass \( m \) is displaced by a small distance \( dr \) against the gravitational attraction force, the work done in this process is given by,
\( F\cdot\,dr=G\frac{Mm}{r^2}\cdot\,dr \).
Hence the total work done in projecting the body from the surface of the earth to an infinite distance, i.e, away from the gravitational influence is given by,
\( W=\displaystyle\int_R^{\infty}F\cdot\,dr \\=\displaystyle\int_R^{\infty}\frac{GMm}{r^2}\,dr \\=GMm\displaystyle\int_R^{\infty}\frac{dr}{r^2} \\=-GMm\left[\frac{1}{x}\right]_R^{\infty} \\=\frac{GMm}{R} \)If the body is projected from the earth’s surface with kinetic energy which is greater than the above value of the potential energy, then the body will escape from the influence of the earth’s gravitational attraction. If \( v_e \) is the escape velocity, then
\( \frac{1}{2}m{v_e}^2=\frac{GMm}{R} \\or,\ v_e=\sqrt{\frac{2GM}{R}}=\sqrt{2\frac{GM}{R^2}R}\\or,\ v_e=\sqrt{2gR} \)where, \( g=\frac{GM}{R^2} \) is the acceleration due to gravity.