Gravitational potential:

The amount of work done in bringing a unit mass from infinity to any point in the gravitational field is called the gravitational potential at that point.

Gravitational potential due to a point mass:

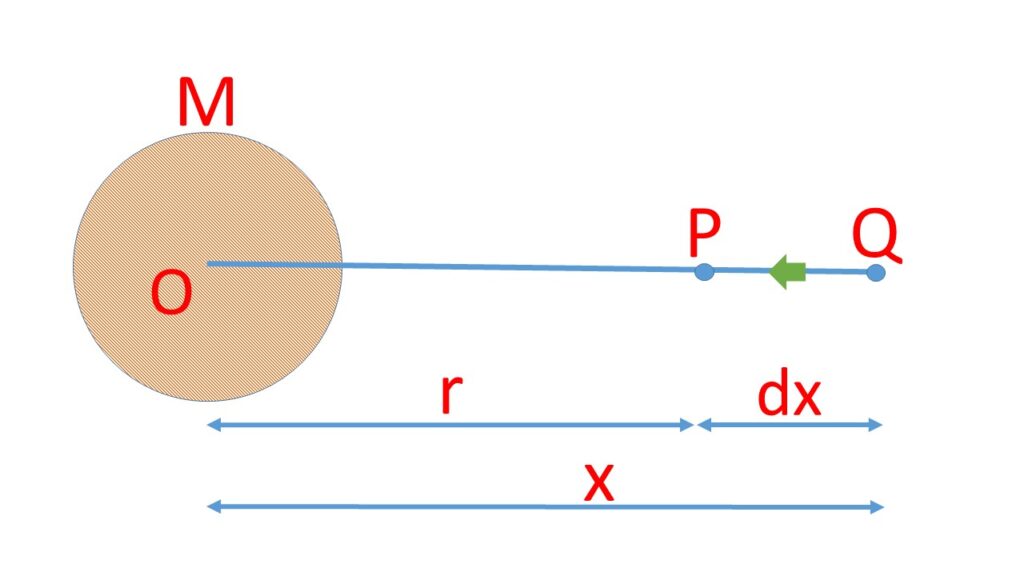
Let the gravitational field is created due to a particle of mass \( M \) at point O. Let us calculate the gravitational potential at point P at a distance \( r \) from the particle of mass \( M \).

Let us consider a unit mass at the point Q, at a distance \( x \) from the point O. Now the force of attraction on the unit mass at the point Q due to mass \( M \) is \( \frac{GM}{x^2} \). Where \( G \) is the gravitational constant. Nw the work done in moving this unit mass from the point Q to the point P a distance \( dx \) in the direction of the force of attraction is \( \frac{GM}{x^2}{dx} \).

Now the total work done in moving the unit mass from infinity to the point P is

\begin{align}
\begin{split}
\displaystyle\int_{\infty}^{r}\frac{GM}{x^2} = GM\displaystyle\int_{\infty}^{r}\frac{dx}{x^2}
\\=GM\left(-\frac{1}{x}\right)\big|_\infty^r 
\\=-GM\left(\frac{1}{r}-\frac{1}{\infty}\right)
\\=-\frac{GM}{r}
\end{split}
\end{align}

So the gravitational potential at a point P is \( V=-\frac{GM}{r} \)