Unit Vectors In Spherical Polar Co-Ordinate System:
In spherical polar co-ordinate system, there are three unit vectors,
- Radial unit vector \( \hat{r} \) along the direction of radius vector \( \vec{r} \).
- \( \hat{\theta} \) along the direction increasing \( \theta \).
- \( \hat{\phi} \) along the direction of increasing \( \phi \).
The unit vector \( \hat{\theta} \) is perpendicular to unit vector \( \hat{r} \).
The unit vector \( \hat{\phi} \) is perpendicular to the both unit vectors \( \hat{r} \) and \( \hat{\theta} \).
In three-dimensional Cartesian co-ordinate, \( \hat{i} \), \( \hat{j} \) and \( \hat{k} \) are the unit vectors along X-axis, Y-axis, and Z-axis respectively.
Unit vector \( \hat{r} \) in terms of \( \hat{i} \), \( \hat{j} \), \( \hat{k} \):
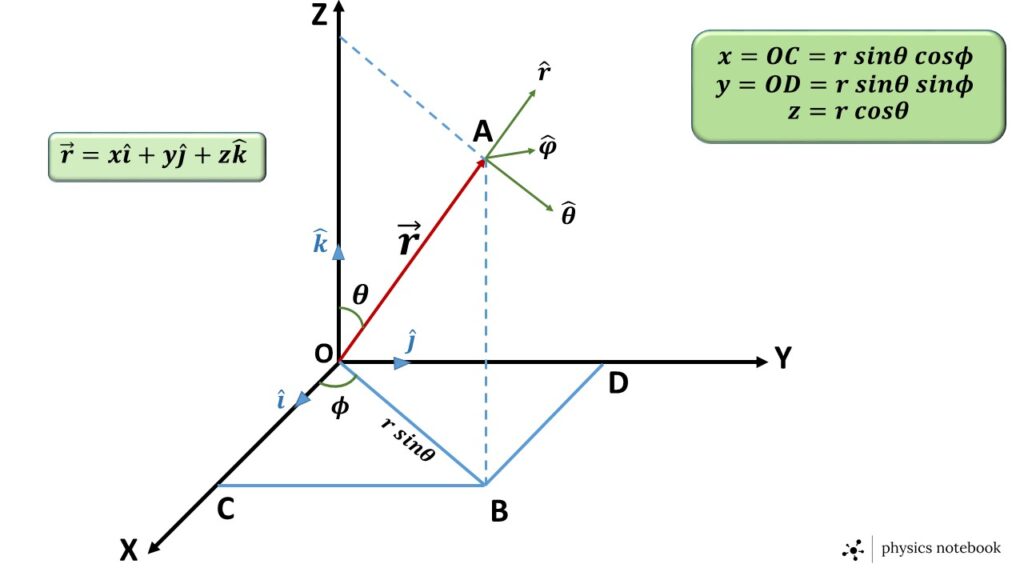
Let us consider a point A having three-dimensional Cartesian co-ordinates \( (x,y,z) \) and spherical polar co-ordinates \( (r,\theta,\phi) \), with respect to the origin O, as shown in the figure 1.
The unit vector \( \hat{r} \) acts along the radial vector \( \vec{r}=\vec{OA} \)
The unit vector \( \hat{\theta} \) acts in the direction of increasing \( \theta \) and is perpendicular to the \( \vec{OA} \),
In three dimensional cartesian co-ordinate,
In spherical polar co-ordinate system,
\( x=r\sin\theta\ \cos\phi \)
\( y=r\sin\theta\ \sin\phi \)
\( z=r\cos\theta \)
Therefore, \( \vec{r}=r\ \sin\theta\ \cos\phi\ \hat{i}+r\ \sin\theta\ \sin\phi\ \hat{j}+r\ \cos\theta\ \hat{k} \).
The unit vector, \( \displaystyle{\hat{r}=\frac{\vec{r}}{|\vec{r}|}} \)
or, \( \displaystyle{\hat{r}=\frac{ r\ \sin\theta\ \cos\phi\ \hat{i}+r\ \sin\theta\ \sin\phi\ \hat{j}+r\ \cos\theta\ \hat{k}}{r}} \)
or, \( \displaystyle{\hat{r}=\sin\theta\ \cos\phi\ \hat{i}+\sin\theta\ \sin\phi\ \hat{j}+\cos\theta\ \hat{k}} \)
Unit vector \( \hat{\theta} \) in term of \( \hat{i} \), \( \hat{j} \), \( \hat{k} \):
Since unit vectors \( \hat{r} \) and \( \hat{\theta} \) are mutually perpendicular to each other and \( \hat{\theta} \) leads \( \hat{r} \) by an angle \( \frac{\pi}{2} \), so we can write,
\( \hat{\theta}=\sin(\theta+\frac{\pi}{2})\ \cos\phi\ \hat{i}+\sin(\theta+\frac{\pi}{2})\ \sin\phi\ \hat{j}+\cos(\theta+\frac{\pi}{2})\ \hat{k} \)or, \( \hat{\theta}=\cos\theta\ \cos\phi\ \hat{i}+\cos\theta\ \sin\phi\ \hat{j}-\sin\theta\ \hat{k} \).
Unit vector \( \hat{\phi} \) in term of \( \hat{i} \), \( \hat{j} \), \( \hat{k} \):
AB is perpendicular to the plane X-Y and \( OB=r\ \sin\theta \) as shown in figure 1.
Let \( \vec{OB} \) is represented by \( \vec{\rho} \)
Now the unit vector \( \hat{phi} \) is perpendicular to the unit vector \( \hat{\rho} \) and \( \hat{\phi} \) leads \( \hat{\rho} \) by an angle \( \frac{\pi}{2} \),
Therefore, \( \vec{\rho}=\rho\ \cos\phi\hat{i}+\rho\ \sin\phi\ \hat{j}\)
So the unit vector along the direction of the vector \( \vec{\rho} \) is given by,
\( \displaystyle{\hat{\rho}=\frac{\vec{\rho}}{\rho}=\cos\phi\ \hat{i}+\sin\phi\ \hat{j}} \)Now, \( \hat{\phi}=\cos(\phi+\frac{\pi}{2})\ \hat{i}+\sin(\phi+\frac{\pi}{2})\ \hat{j} \)
or, \( \hat{\phi}=-\sin\phi\ \hat{i}+\cos\phi\ \hat{j} \).