Strain:

When a force or a system of forces acting upon a body produces a relative displacement between its parts and the change in length, volume, or shape may take place, then the body is said to be under the strain. The strain of a body is measured in the form of dimension per unit dimension, this means that the ratio of length, volume, or shape to the original length, volume, or shape. Since the strain is the ratio of two same quantity, so it is a pure number without dimension. It has no unit.

Stress:

When a body is under strain, the internal forces of reaction are automatically set up within the body. Since this acts in the opposite direction, the body always tends to return to its original dimension, i.e, length, volume, or shape, as soon as the deforming forces are withdrawal. This restoring force per unit area is called stress. According to Newton’s law of reaction, numerically this restoring force is equal to the deforming force, so long as the strain is produced within the elastic limit.

Stress is measured by the applied force per unit area,

Stress = \frac{F}{\alpha}

where \( F \) is the total applied force on a surface of total area \( \alpha \).

Stress is measured in \( N/m^2 \), \( dyne/{cm}^2 \), \( poundal/{ft}^2 \).

The dimension of stress is \( [ML^{-1}T^{-2}] \).

What will happend when the force is inclind to the surface?

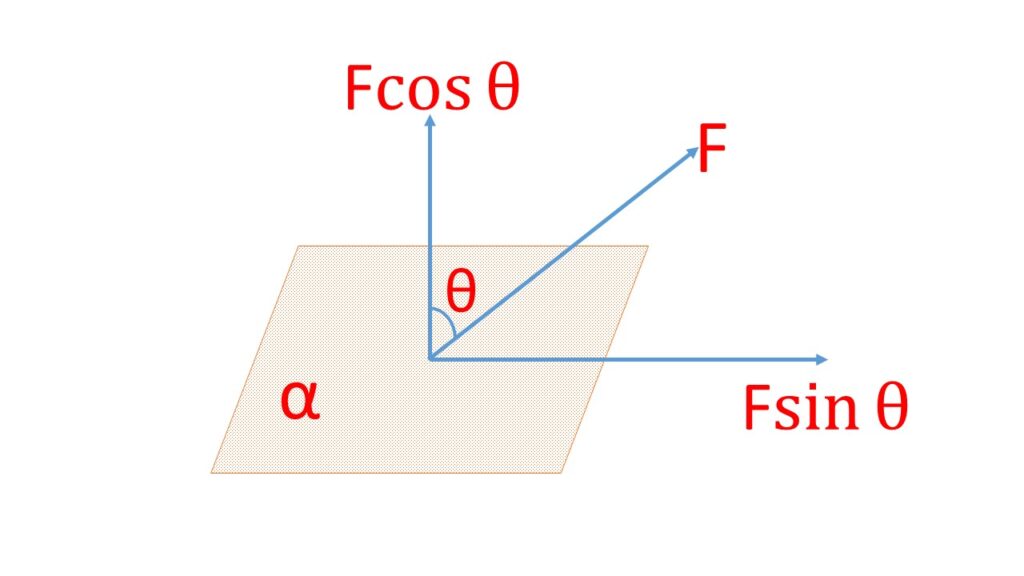
• If the force is inclined to the surface then the component of the force perpendicular to the surface per unit area is called ‘normal stress‘.
• The component acting along the surface per unit area is called the ‘tangential stress’ or ‘shearing stress’

Let \( F \) is the force, acting at an angle \( \theta \) with the normal to the surface of area \( \alpha \) , then

Normal Stress = \frac{F{\cdot}Cos\theta}{\alpha}

Shearing Stress = \frac{F{\cdot}Sin{\theta}}{\alpha} 

The stress is always normal in case of a change in length of the wire or in case of a change in the volume of a body but is tangential in case of a change in the shape of a body.