The angle of contact between a liquid and a solid surface depends upon
- the nature of the solid and the liquid,
- the medium above the free surface of the liquid.
The angle of contact does not depend upon the angle of inclination of the solid to the free surface of the liquid, within which the solid is dipped in the liquid.
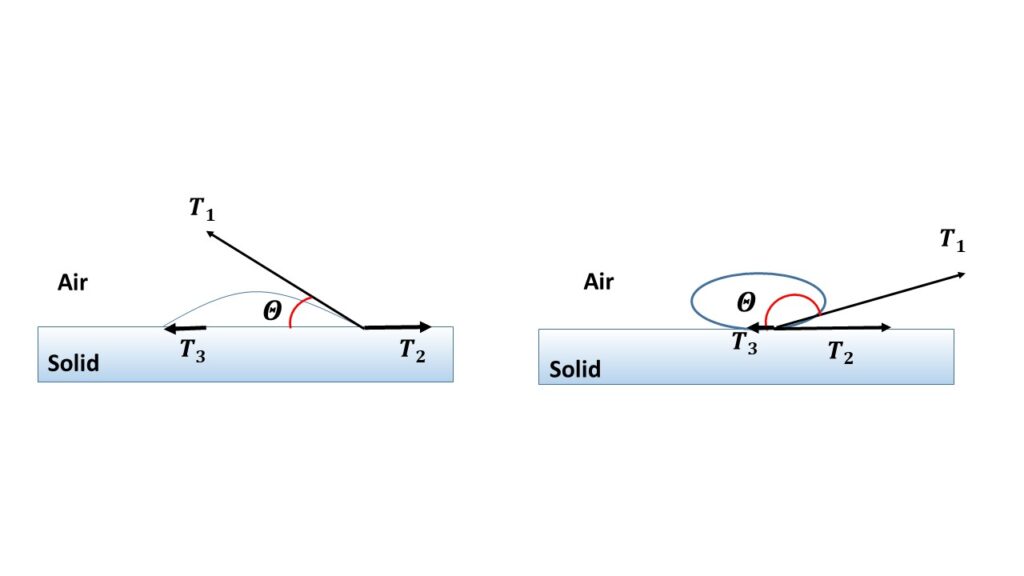
To find whether the angle of contact between a solid and a liquid is obtuse or acute, let us consider the case of a solid, liquid and air in contact. Let \( \theta \) be the angle of contact and \( T_1 \) be the surface tension of the air-liquid interface, \( T_2 \) be the surface tension of the air-solid interface and \( T_3 \) be the surface tension of the liquid-solid interface respectively as shown in the figure.
In equilibrium,
\( T_3+T_1\cos\theta=T_2\\or,\ \cos\theta=\frac{T_2-T_3}{T_1} \)- If \( T_2>T_3 \), \( \cos\theta \) is positive and \( \theta<90^\circ \) (acute)
- If \( T_2<T_3 \), \( \cos\theta \) is negative and \( \theta>90^\circ \) (obtuse)
- If \( T_2-T_3>T_1 \) or, \( T_2>T_3+T_1 \), \( \cos\theta>1 \) which is positive.
So there will be no equilibrium and the liquid will spread over the solid.