Two Particles Of Masses ‘m’ And ‘M’ Are At A Distance ‘d’ Apart. Calculate The Moment Of Inertia Of The System About An Axis Passing Through The Centre Of Mass And Perpendicular To The Line Joining The Two Masses. If ‘ν’ Be The Frequency Of Revolution, Then Also Calculate The Rotational Kinetic Energy Of The System.

Share:

Ans.

Fig. 1

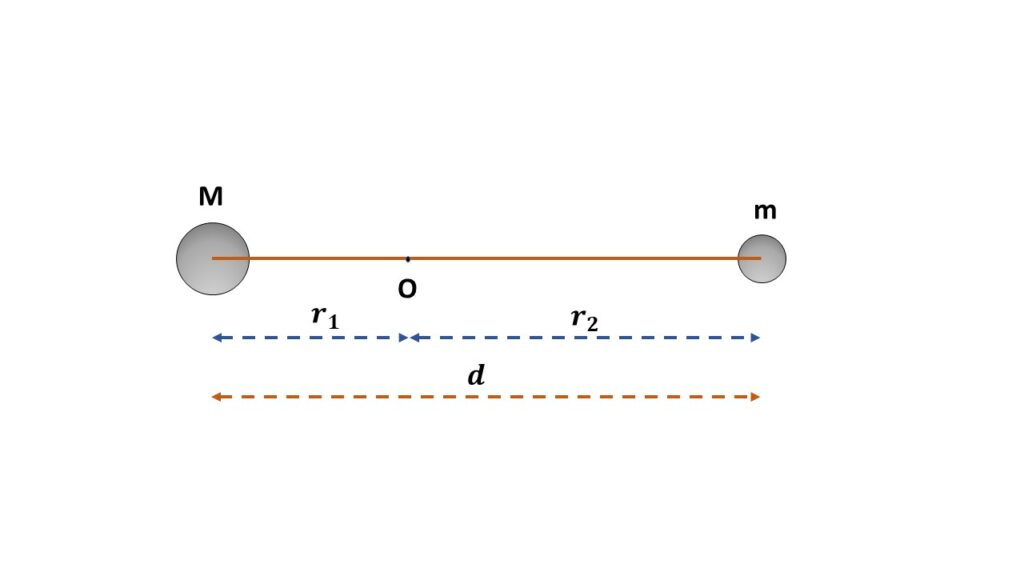
Here the two masses ‘m‘ and ‘M‘ are at a distance d apart.
Let us consider, O be the centre of mass of the system of these two masses, \( r_1 \) be the distance of mass M from the centre of mass O and \( r_2=(d-r_1) \) be the distance of m from the centre of mass O.

So we have, \( Mr_1=mr_2 \)

or, \( Mr_1=m(d-r_1) \)

or, \( Mr_1+mr_1=md \)

or, \( \displaystyle{r_1=\frac{md}{M+m}} \)

Again, \( r_2=d-r_1 \)

or, \( r_2=d-\frac{md}{M+m} \)

or, \( \displaystyle{r_2=\frac{Md}{M+m}} \)

So the moment of inertia of the system through the centre of mass O and perpendicular to the line joining the two masses is

\( I=Mr_1^2+mr_2^2 \)

or, \( I=M{\left(\frac{md}{M+m}\right)}^2+m{\left(\frac{Md}{M+m}\right)}^2 \)

or, \( \displaystyle{I=\frac{Mm^2+mM^2}{{(M+m)}^2}d^2} \)

or, \( \displaystyle{I=\frac{Mm}{M+m}d^2} \)

or, \( \displaystyle{I=\mu{d^2}} \)

Where, \( \mu=\frac{Mm}{M+m} \), is the reduced mass of the system.

Now the rotational kinetic energy of the system is given by,

\( T=\frac{1}{2}I{\omega}^2 \)

or, \( T \) \( =\displaystyle{\frac{1}{2}\mu{d^2}{\omega}^2\\=\frac{1}{2}\frac{Mm}{M+m}d^2(4{\pi}^2{\nu}^2)\\=2{\pi}^2{\nu}^2\frac{Mm}{M+m}d^2} \)

Where, angular velocity \( \omega=2\pi\nu \)

Share:
Tags: