Ans.

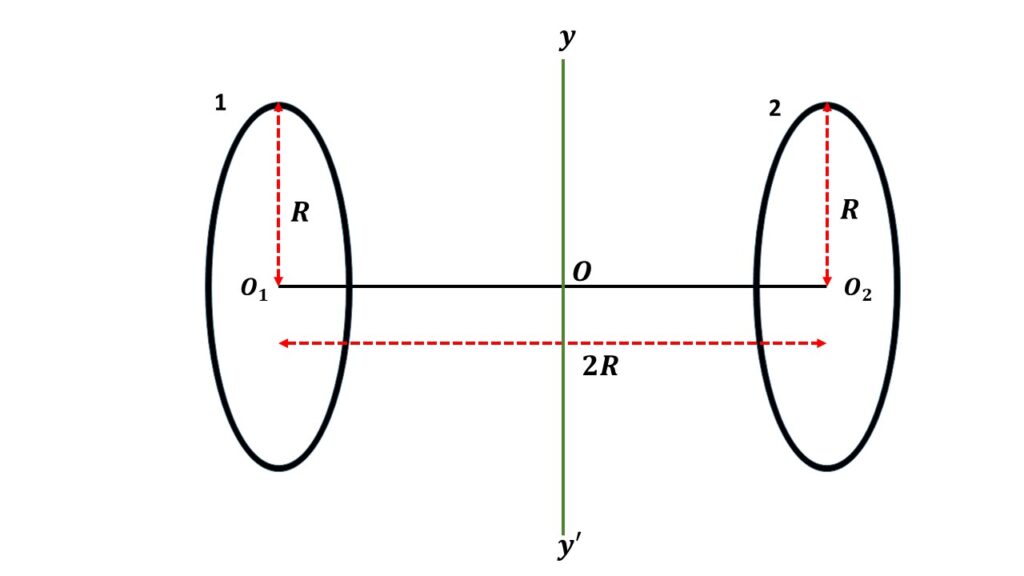
Here, two wheels each of mass M and radius R are rigidly connected by a weightless rod of length 2R.
The moment of inertia of each wheel about their diameter is \( \frac{1}{2}MR^2 \).
[ To know the derivation of moment of inertia of a wheel about its own diameter, ( CLICK HERE ) ]

By applying the theorem of parallel axes, the moment of inertia of each wheel about the axis \( yy’ \) passing through the centre o and perpendicular to the length of the rod \( O_1O_2 \) is given by,

\( \frac{1}{2}MR^2+MR^2\\=\frac{3}{2}MR^2 \)

So the moment of inertia of the both wheel about the axis \( yy’ \) is

\( 2\times{\frac{3}{2}MR^2}=3MR^2 \)