Two concentric spherical shells of masses \( M_1 \) and \( M_2 \) have uniform density \( \sigma \). These two spherical shells behave as if their masses \( M_1 \) and \( M_2 \) are concentrated at their common centre.

(i) At the point r=a:

The magnitude of the gravitational fields at r=a due to \( M_1 \) and \( M_2 \) are \( \frac{GM_1}{a^2} \) and \( \frac{GM_2}{a^2} \) respectively, both are directed along the line joining the common centre and the point \( r=a \). [where \( G \) is the gravitational constant.]

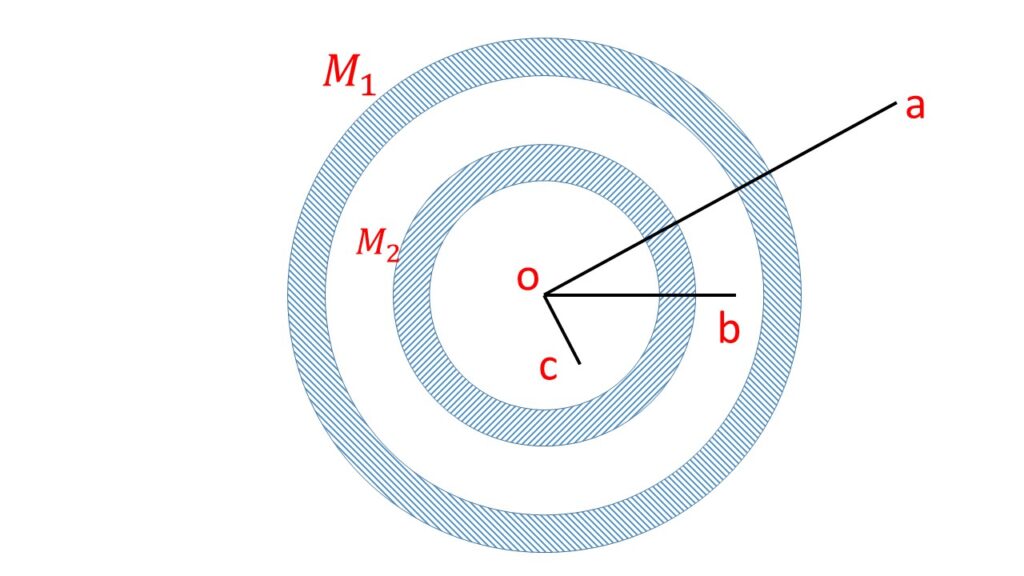
Hence the magnitude of the resultant field is \( \frac{G(M_1+M_2)}{a^2} \). So the force on the particle of mass \( m \), placed at the point \( a \) is \( \frac{G(M_1+M_2)}{a^2}\cdot{m} \).

(ii) At the point r=b:

The point \( r=b \) is an external point with respect to the shell \( M_2 \) and an internal point with respect to the shell \( M_1 \). Since the gravitational field intensity at an internal point due to a shell is zero. So here the gravitational field intensity at \( r=b \) is due to only shell \( M_2 \) which behaves as if its entire mass is at centre. The magnitude of the gravitational field intensity is \( \frac{GM_2}{b^2} \). Now the force on the particle of mass \( m \) at \( r=b \) is \( \frac{GM_2}{b^2}\cdot{m} \).

(iii) At the point r=c:

The point \( r=c \) is the internal point due to the both shells \( M_1 \) and \( M_2 \). Since the gravitational field intensity at a point inside the shell is zero, So the gravitational field intensity at the point \( r=c \) due to the both shells is \( zero \).