Gravitational Potential Due To A Thin Uniform Spherical Shell:

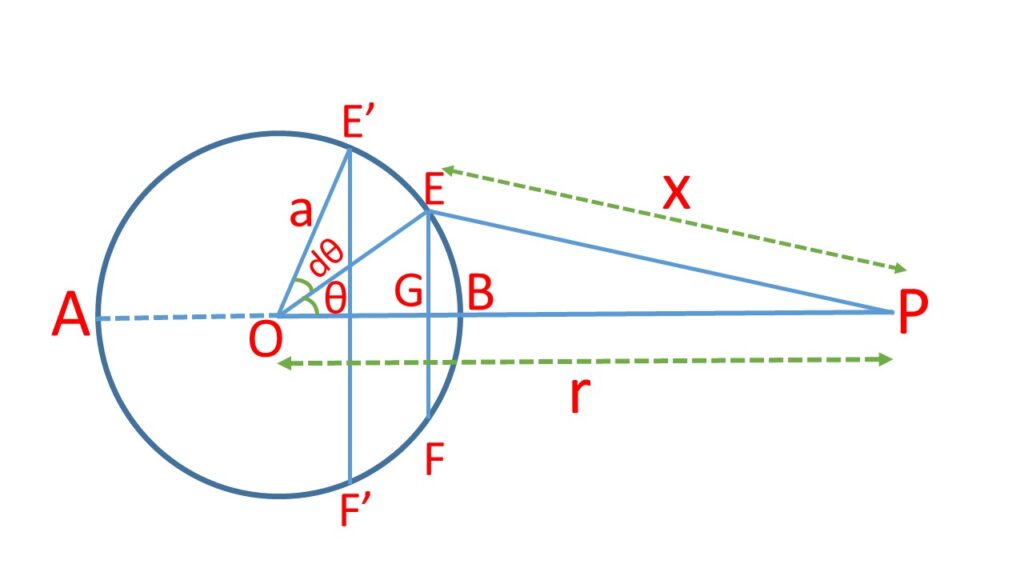
The surface area of the ring is \( 2\pi{\cdot}a\sin\theta{\cdot}a\ d\theta = 2\pi{a^2}\sin\theta{d}\theta \)

Mass of the ring is \( 2\pi{a^2}\sin\theta\ d\theta{\cdot}\sigma \)

Gravitational potential at \( P \) due to the ring is \( \displaystyle{dv=-G\frac{2\pi{a^2}\sin\theta\ d\theta\ \sigma}{x}} \).

where \( x \) is the distance of every point on the rim of the ring, \( G \) is the gravitational constant.

Now from \( \triangle{EOP} \),

\( {EP}^2 \\={OE}^2+{OP}^2-2\ {(OE)}\ {(OP)}\ \cos\theta \)

or, \( x^2=a^2+r^2+2ar\cos\theta \)

Differentiating both side, \( 2x\,dx=2ar\sin\theta\,d\theta \), where \( a \) and \( r \) are the constants.

\( or,\ x\,dx=ar\sin\theta\,d\theta \\ or,\ \sin\theta\,d\theta=\frac{x}{ar}\,dx \)

\( \displaystyle{\,dv=-G\frac{2\pi{a\sigma}}{r}\,dx} \)

(i) When the point \( P \) is outside the shell.

The total potential at \( P \) is given by,

\( V=-G\frac{2\pi{a}\sigma}{r}\displaystyle\int_{r-a}^{r+a}\,dx \\= -G\frac{2\pi{a}\sigma}{r} (r+a-r+a)\\= -G\frac{2\pi{a}\sigma}{r}2a\\= -G\frac{4\pi{a}^2\sigma}{r} \) \( or,\ V=-\displaystyle\left(\frac{GM}{r}\right) \)

where \( M=4\pi{a}^2\sigma \) is the total mass of the thin spherical shell.

Here, for an external point, the spherical shell behaves as if its whole mass is concentrated at the centre.

(ii) When the point \( P \) is on the surface of the shell:

In this case \( r=a \), and the total potential at \( P \) is given by,

\( V= -G\frac{2\pi{a}\sigma}{r}\displaystyle\int_{0}^{2a}\,dx \\ = -G\frac{2\pi{a}\sigma}{r}2a\\= -G\frac{4\pi{a}^2\sigma}{r} \)

\( or,\ V=-\frac{GM}{r} \) \( or,\ V=-\displaystyle{\frac{GM}{a}} \)

In this case also the mass of the shell may be considered to be concentrated at the centre of the shell.

(iii) When the point \( P \) is inside the shell:

Now the point \( P \) is inside the shell, so the total potential at \( P \) is given by,

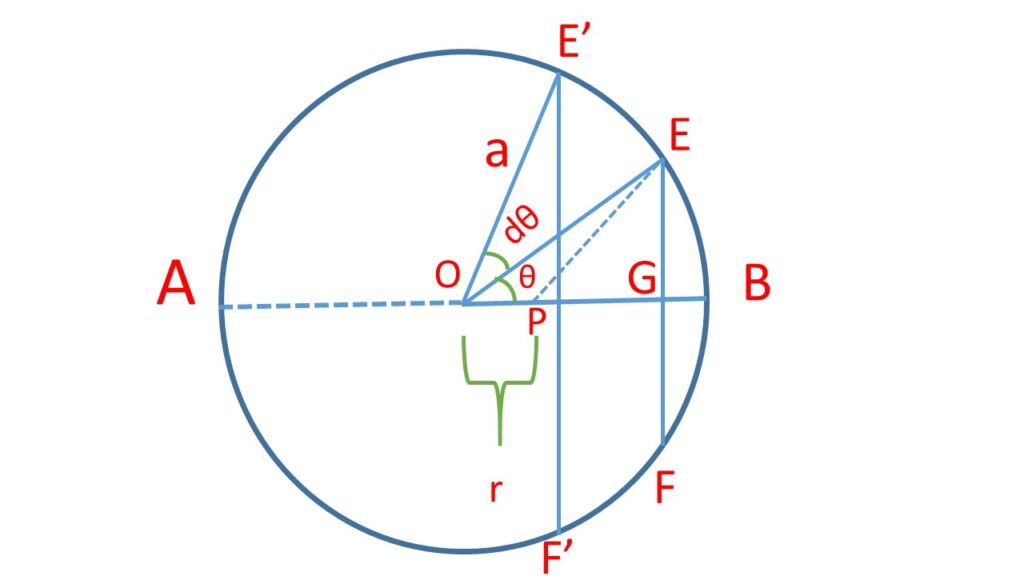
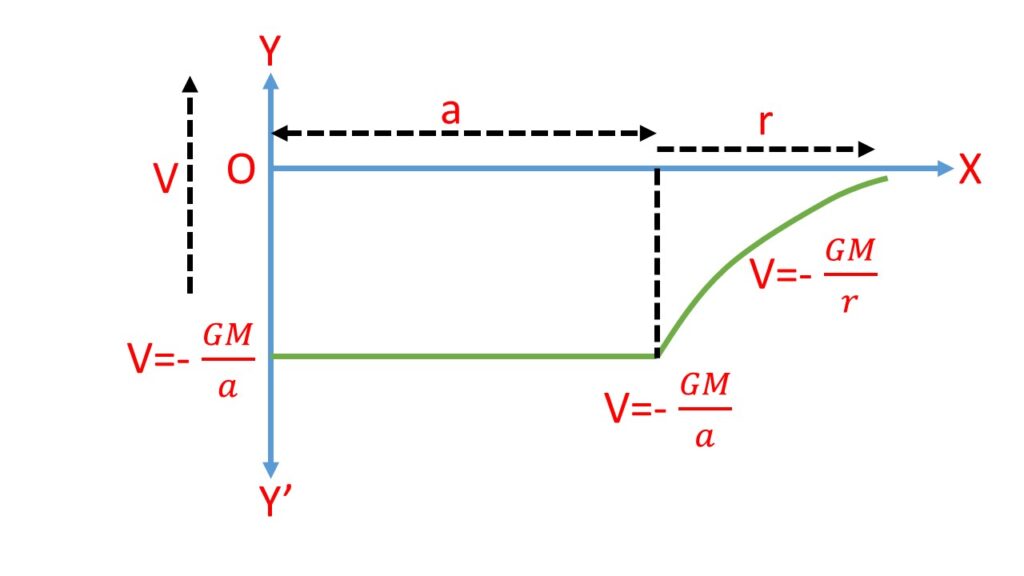
Thus the potential at any point inside shell is consant and is equal to that of the surface.