Unit vectors in spherical polar co-ordinate system are mutually perpendicular to each other:

Two unit vectors are said to be orthogonal to each other when the angles between these two unit vectors are \( 90^{\circ} \), i.e., they are perpendicular to each other.

In order to prove the unit vectors (\( \hat{r} \), \( \hat{\theta} \), \( \hat{\phi} \)) in spherical polar co-ordinate system are mutually perpendicular to each other, we have to prove that the angles between \( \hat{r} \) & \( \hat{\theta} \), \( \hat{\theta} \) & \( \hat{\phi} \), \( \hat{r} \) & \( \hat{\phi} \) are \( 90^{\circ} \) each.

Let us consider a point A having spherical polar co-ordinate (\( r,\theta,\phi \)) as shown in figure 1.

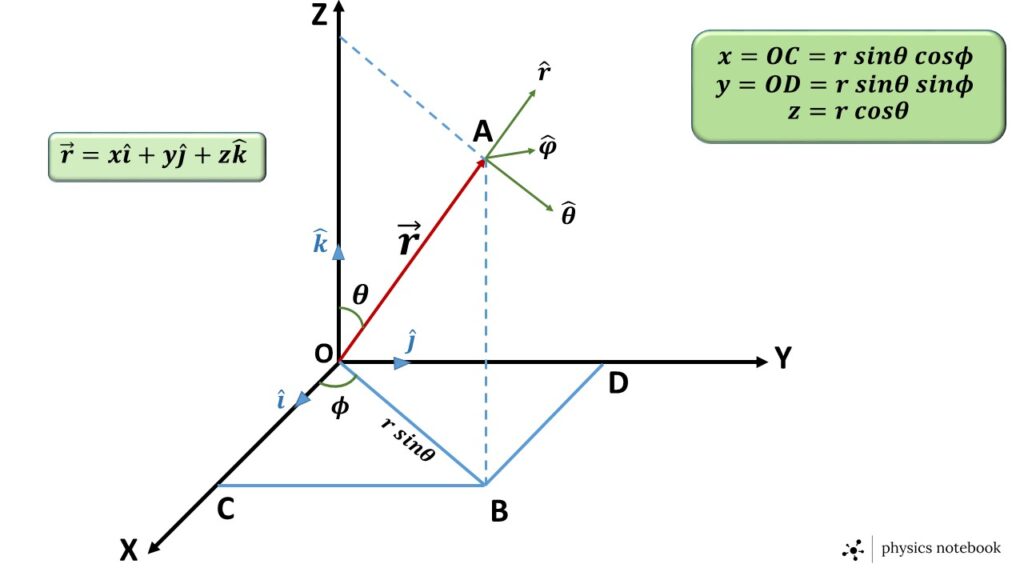
The unit vectors in three-dimensional polar co-ordinate system are \( \hat{r} \), \( \hat{\theta} \) , \( \hat{\phi} \).

So we can write,

\( \hat{r}=\sin\theta\ \cos\phi\ \hat{i}+\sin\theta\ \sin\phi\ \hat{j}+\cos\theta\ \hat{k} \)

\( \hat{\theta}=\cos\theta\ \cos\phi\ \hat{i}+\cos\theta\ \sin\phi\ \hat{j}-\sin\theta\ \hat{k} \)

\( \hat{\phi}=-\sin\phi\ \hat{i}+\cos\phi\ \hat{j} \)

where, \( \hat{i}.\hat{j},\hat{k} \) are the unit vectros in the three-dimensional cartesian co-ordinate system along X-axis, Y-axis and Z-axis respectively.

[ To know the derivation of the above unit vectors, CLICK HERE ]

Angle between \( \hat{r} \) & \( \hat{\theta} \):

The scaler product of \( \hat{r} \) & \( \hat{\theta} \) is given by,

\( \hat{r}\cdot\hat{\theta}=(\sin\theta\ \cos\phi\ \hat{i}+\sin\theta\ \sin\phi\ \hat{j}+\cos\theta\ \hat{k})\cdot(\cos\theta\ \cos\phi\ \hat{i}+\cos\theta\ \sin\phi\ \hat{j}-\sin\theta\ \hat{k}) \)

or, \( \hat{r}\cdot\hat{\theta}=\sin\theta\ \cos\theta\ {\cos}^2\phi+\sin\theta\ \cos\theta\ {\sin}^2\phi-\cos\theta\ \sin\theta \)

or, \( \hat{r}\cdot\hat{\theta}=\sin\theta\ \cos\theta({\cos}^2\phi+{\sin}^2\phi)-\sin\theta\ \cos\theta \)

or, \( \hat{r}\cdot\hat{\theta}=\sin\theta\ \cos\theta-\sin\theta\ \cos\theta \)

or, \( \hat{r}\cdot\hat{\theta}=0 \)

[where, \( \hat{i}\cdot\hat{j}=\hat{j}\cdot\hat{k}=\hat{i}\cdot\hat{k}=0 \) and \( \hat{i}\cdot\hat{i}=\hat{j}\cdot\hat{j}=\hat{k}\cdot\hat{k}=1 \)]

So the angle between \( \hat{r} \) and \( \hat{\theta} \) is \( 90^{\circ} \), i.e., the unit vectors \( \hat{r} \) and \( \hat{\theta} \) are perpendicular to each other.

Angle between \( \hat{\theta} \) & \( \hat{\phi} \):

The scalar product of the unit vectors \( \hat{\theta} \) and \( \hat{\phi} \) is given bellow,

\( \hat{\theta}\cdot\hat{\phi}=(\cos\theta\ \cos\phi\ \hat{i}+\cos\theta\ \sin\phi\ \hat{j}-\sin\theta\ \hat{k})\cdot(-\sin\phi\ \hat{i}+\cos\phi\ \hat{j}) \)

or, \( \hat{\theta}\cdot\hat{\phi}=-\cos\theta\ \sin\phi\ \cos\phi+\cos\theta\ \sin\phi\ \cos\phi \)

or, \( \hat{\theta}\cdot\hat{\phi}=0 \)

So the angle between the unit vectors \( \hat{\theta} \) & \( \hat{\phi} \) is  \( 90^{\circ} \), i.e., the unit vectors \( \hat{\theta} \) & \( \hat{\phi} \) are perpendicular to each other.

Angle between \( \hat{r} \) & \( \hat{\phi} \):

The scalar product of the unit vectors \( \hat{r} \) and \( \hat{\phi} \) is given bellow,

\( \hat{r}\cdot\hat{\phi}=(\sin\theta\ \cos\phi\ \hat{i}+\sin\theta\ \sin\phi\ \hat{j}+\cos\theta\ \hat{k})\cdot(-\sin\phi\ \hat{i}+\cos\phi\ \hat{j}) \)

or, \( \hat{r}\cdot\hat{\phi}=-\sin\theta\ \sin\phi\ \cos\phi+\sin\theta\ \sin\phi\ \cos\phi \)

or, \( \hat{r}\cdot\hat{\phi}=0 \)

So the angle between the unit vectors \( \hat{r} \) & \( \hat{\phi} \) is \( 90^{\circ} \), i.e., the unit vectors \( \hat{r} \) & \( \hat{\phi} \) are perpendicular to each other.

Therefore the unit vectors \( \hat{r} \), \( \hat{\theta} \) and \( \hat{\phi} \) in the spherical polar co-ordinate system are mutually perpendicular to each other.