A shear is equivalent to a compression and an extension at right angle to each other:
Let us consider a cube \( PQRS \), having each side equal to \( L \) with its lower face \( SR \) is fixed.
Let us consider a tangential force \( F \) is applied on the upper face \( PQ \), so that the cube is sheared to the new position \( P’Q’RS \) through an angle \( \theta \). Now \( PP’=QQ’=l \).
Diagonal \( SQ \) is elongated to \( SQ’ \) and the diagonal \( RP \) is contracted to \( RP’ \).
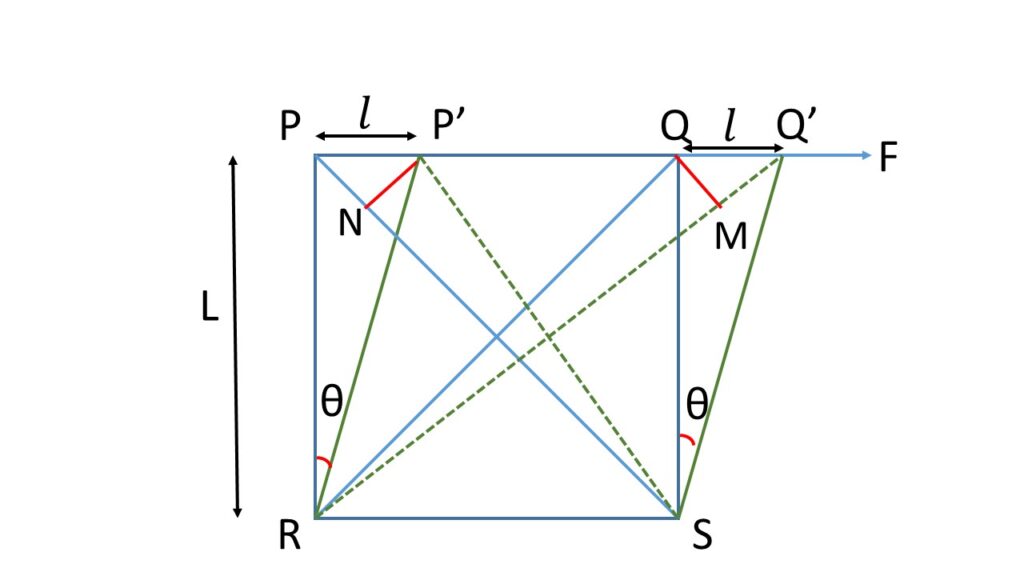
Let the perpendiculars \( P’N \) on \( PR \) and \( QM \) on \( SQ’ \) are drawn.
Since the angle of shear \( \theta \) is very small,
Therefore, \( \triangle{PNP’} \) and \( \triangle{QMQ’} \) are right angle triangles.
Therefore, \( \angle{P’PN} \) = \( \angle{QQ’M} \)= \( 45^\circ \)
Now, the extensional strain alonge the diagonal \( SQ \) is,
\( \frac{MQ’}{SM}=\frac{MQ’}{SQ}\\=\frac{(QQ’)\cos\angle{MQ’Q}}{\sqrt{2}L} \\=\frac{l\cos{45^\circ}}{\sqrt{2}L} \\=\displaystyle{\frac{l/\sqrt{2}}{\sqrt{2}L}} \\=\displaystyle{\frac{1}{2}\frac{l}{L}} \\=\displaystyle{\frac{1}{2}\theta}\)Similarly the compression strain along the diagonal \( PR \) is,
\( \displaystyle{\frac{PN}{RP}}\\=\displaystyle{\frac{(PP’)\cos\angle{P’PN}}{RP}} \\=\frac{l\cos{45^\circ}}{RP} \\=\displaystyle{\frac{l/\sqrt{2}}{\sqrt{2}L}} \\=\displaystyle{\frac{1}{2}\frac{l}{L}} \\=\displaystyle\frac{1}{2}\theta\)Both the extention and contraction are at \( 45^\circ \) to \( PQ \) and \( RS \), hence they are mutually at right angle.
So a shear is equivalent to an extensional and compressional strain and at right angle to each other.