The centre of suspension and oscillation are reversible:
In Fig. 1, the point O is called the centre of suspension, where the horizontal axis of rotation of the compound pendulum meets the vertical plane of oscillation of that compound pendulum.
O’ is called the centre of oscillation for the given centre of suspension O of the compound pendulum, where the mass of the compound pendulum may be considered to be concentrated without causing any change in the time period, for a given centre of suspension (O).
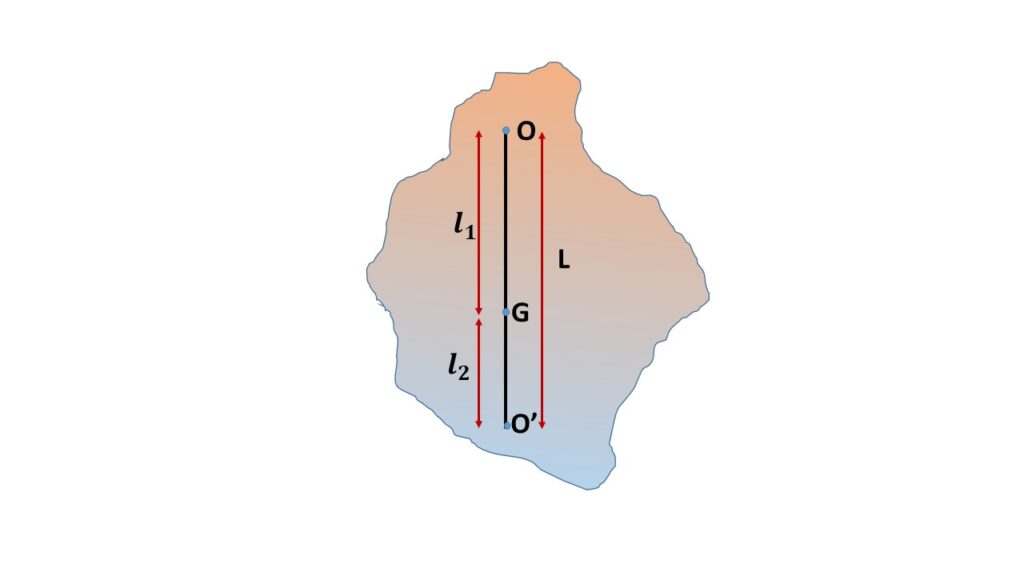
If the time period of oscillation of the compound pendulum about the point of suspension O is the same as the the time period of oscillation of that compound pendulum taking point of oscillation O’ as point of suspension, then pendulum is called the reversible.
Let \( T_1 \) be the time period of oscillation of the compound pendulum, when we take O as the point of oscillation,
\( \displaystyle{T_1=2\pi\sqrt{\frac{K^2+l_1^2}{l_1g}}} \)
where, \( l_1=OG \), \( G \) is the centre of gravity of the compound pendulum, \( K \) is the radius of gyration of the compound pendulum. \( g \) is the acceleration due to gravity.
Since, \( \displaystyle{L=\frac{K^2+l_1^2}{l_1}} \)
Therefore, \( \displaystyle{T_1=2\pi\sqrt{\frac{L}{g}}} \)
Again \( L=l_1+l_2 \), where \( L_2 =GO’\)
\( \displaystyle{T_1=2\pi\sqrt{\frac{l_1+l_2}{g}}} \)
So, \( \frac{K^2+l_1^2}{l_1}=l_1+l_2 \)
or, \( K^2+l_1^2=l_1^2+l_1l_2 \)
or, \( K^2=l_1l_2 \)
When we take \( O’ \) as the point of suspension, then the time period of oscillation about that point \( O’ \) is
\( \displaystyle{T_2=2\pi\sqrt{\frac{K^2+l_2^2}{l_2g}}} \)
or, \( \displaystyle{T_2=2\pi\sqrt{\frac{l_1l_2+l_2^2}{l_2g}}} \)
or, \( \displaystyle{T_2=2\pi\sqrt{\frac{l_1+l_2}{g}}} \)
or, \( \displaystyle{T_2=2\pi\sqrt{\frac{L}{g}}} \)
or, \( T_2=T_1 \)
Thus the two time periods of oscillation are same.
So the centre of suspension and centre of oscillation of the compound pendulum are reversible.