Ans.

Let us consider a system of n particles of masses \( m_1 \), \( m_2 \), \( \cdots \), \( m_n \) having position vector \( \vec{r_1} \), \( \vec{r_2} \), \( \cdots \), \( \vec{r_n} \) with respect to the origin O.

If \( \vec{r_i} \) be the position vector with respect to the origin O of the ith particle of mass \( m_i \) and \( \vec{v_i} \) be the velocity of that its particle, then the total kinetic energy of the system is given by,

\( T=\frac{1}{2}\displaystyle{\sum_{i=1}^{n}}m_i{\vec{v_i}}^2 \)

or, \( T=\frac{1}{2}\displaystyle{\sum_{i=1}^{n}}m_i(\dot{\vec{r_i}}\cdot\dot{\vec{r_i}})\tag{1} \)

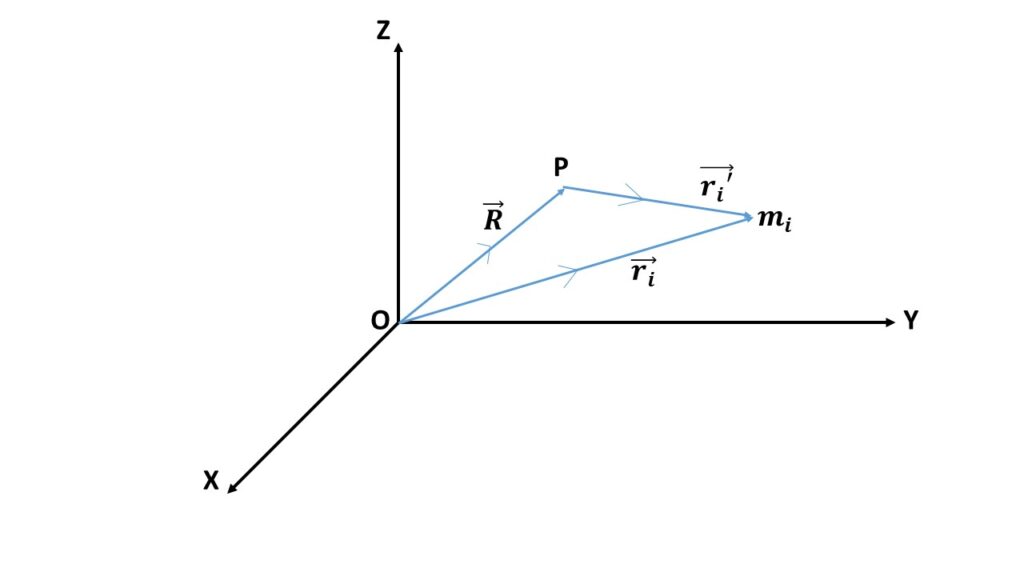
If \( \vec{r_i}’ \) be the position vector of the its particle with respect to the centre of mass point P, then from Fig. 1 we can write,

\( \vec{r_i}=\vec{R}+\vec{r_i}’ \)

Differentiating both side with respect to the time t,

\( \dot{\vec{r_i}}=\dot{\vec{R}}+\dot{\vec{r_i}’} \)

or, \( \dot{\vec{r_i}}=\vec{V}+\vec{v_i}’\tag{2} \)

Using equation (2) in equation (1) we get,

\( T=\frac{1}{2}\displaystyle{\sum_{i=1}^{n}}m_i\left[(\vec{V}+\vec{v_i}’)\cdot(\vec{V}+\vec{v_i}’)\right] \)

= \( \frac{1}{2}\displaystyle{\sum_{i=1}^{n}}m_i(\vec{V}\cdot\vec{V})+\frac{1}{2}\displaystyle{\sum_{i=1}^{n}}m_i(\vec{v_i}’\cdot\vec{v_i}’)+\displaystyle{\sum_{i=1}^{n}}m_i(\vec{V}\cdot\vec{v_i}’) \)

= \( \frac{1}{2}\displaystyle{\sum_{i=1}^{n}}m_iV^2+\frac{1}{2}\displaystyle{\sum_{i=1}^{n}}m_i{\vec{v_i}’}^2+\vec{V}\displaystyle{\sum_{i=1}^{n}}(m_i\vec{v_i}’) \)

=\( \frac{1}{2}MV^2+\frac{1}{2}\displaystyle{\sum_{i=1}^{n}}m_i{\vec{v_i}’}^2 \)

since, \( \displaystyle{\sum_{i=1}^{n}}(m_i\vec{v_i}’)=0 \)