Displacement in spherical polar co-ordinate system:

Let us consider a point A in a three-dimensional cartesian co-ordinate system, the position of this point can be described by a specific single vector. This vector is the displacement of that point A with respect to the origin O of the co-ordinate system, as shown in the figure below.

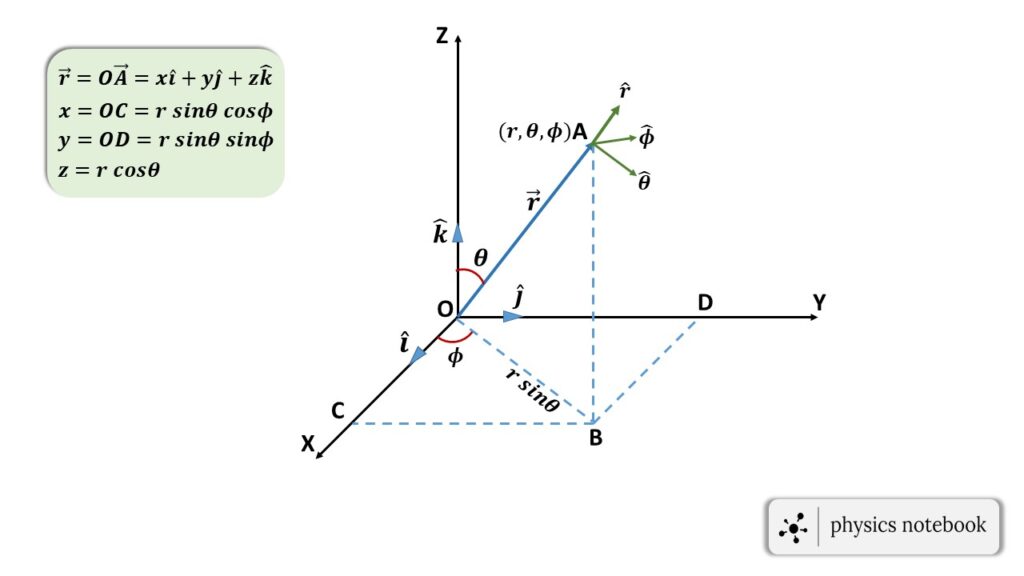
This vector is known as the “position vector” of that point A with respect to the origin O.

Here the position vector is denoted by the \( \vec{OA}=\vec{r} \).

\( \vec{r} \) gives the magnitude as well as the direction of displacement.

If \( \hat{r} \) be the unit vector along \( \vec{r} \), then we can write,

\( \displaystyle{\hat{r}=\frac{\vec{r}}{|\vec{r}|}} \). where, \( |\vec{r}| \) is the magnitude of the vector \( \vec{r} \).

Let, \( (r,\theta,\phi) \) be the spherical polar co-ordinate of the point A with respect to the origin and  \( (x,y,z) \) be the corresponding cartesian co-ordinates of that point A as shown in the figure 1.

therefore, \( \vec{r}=x\hat{i}+y\hat{j}+z\hat{k} \)

where, \( \hat{i},\ \hat{j}, \) & \( \hat{k} \) are the unit vectors along the X-axis, Y-axis and Z-axis respectively.

\( x=r\sin\theta\ \cos\phi \)

\( y=r\sin\theta\ \sin\phi \)

and \( z=r\cos\theta \).

So the displacement can be written as

\( \vec{r}= r\sin\theta\ \cos\phi\ \hat{i}+ r\sin\theta\ \sin\phi\ \hat{j}+ r\cos\theta\ \hat{k} \)

The unit vector \( \hat{r} \) can be written as,

\( \hat{r}= \sin\theta\ \cos\phi\ \hat{i}+ \sin\theta\ \sin\phi\ \hat{j}+ \cos\theta\ \hat{k} \)