The velocity on reaching the earth’s surface of a body which falls freely:
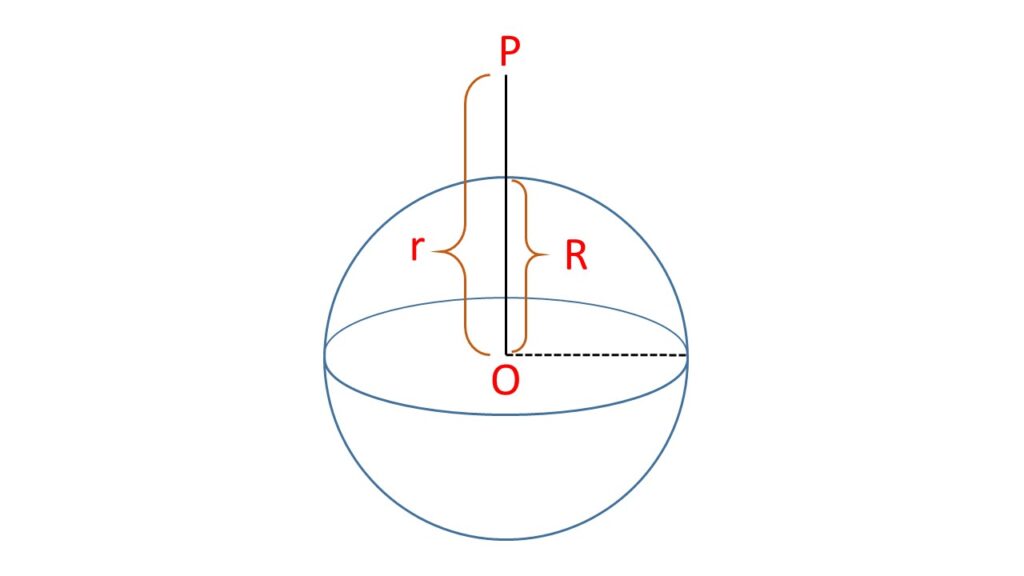
Let us consider the mass of the earth is \( M \) and the radius is \( R \). There is a body of mass \( m \) at a the point \( P \) at a distance \( r \) from the centre \( O \) of the earth.
Now the differential equation of motion of the body is,
\( m\frac{d^2{r}}{dt^2}=-G\frac{Mm}{r^2} \\or,\ \frac{d^2{r}}{dt^2}=-\frac{GM}{r^2}=-\frac{\mu}{r^2} \)where \( G \) is the gravitational constant and \( \mu=GM \).
Multiplying both sides by \( 2\frac{dr}{dt} \), we get
\( 2\frac{dr}{dt}\frac{d^2{r}}{dt^2}=-2\frac{\mu}{r^2}\frac{dr}{dt} \)Integrating both side we get,
\( \left(\frac{dr}{dt}\right)^2=\frac{2\mu}{r}+C \)where \( C \) is the integration constant.
Since the body starts from infinity so the initial velocity of the body is zero, i.e, at \( x=\infty \), \( \frac{dr}{dt}=0 \).
Therefore \( C=0 \).
now, \( \left(\frac{dr}{dt}\right)^2= \frac{2\mu}{r} \).
Again when \( r=R \), \( \frac{dr}{dt}=v \), the velocity at the earth’s surface.
\( v^2=\frac{2\mu}{R} \)or, \( \displaystyle{v=\sqrt{\frac{2GM}{R}}} \)
A body falls freely under \( g \) from a height \( R \):
A body falls freely under constant acceleration due to gravity \( g \) from a height \( R \) which is the radius of the earth. \( v’ \) is the velocity attains by the body then we can write,
\( {v’}^2=0^2+2gR \) (here initial velocity is zero)
or, \( v’=\sqrt{2gR}=\sqrt{2\frac{GM}{R^2}R} \)
or, \( v’=\displaystyle{\sqrt{\frac{2GM}{R}}} \)
Therefore \( v=v’ \).