Condition for minimum time period of compound pendulum:

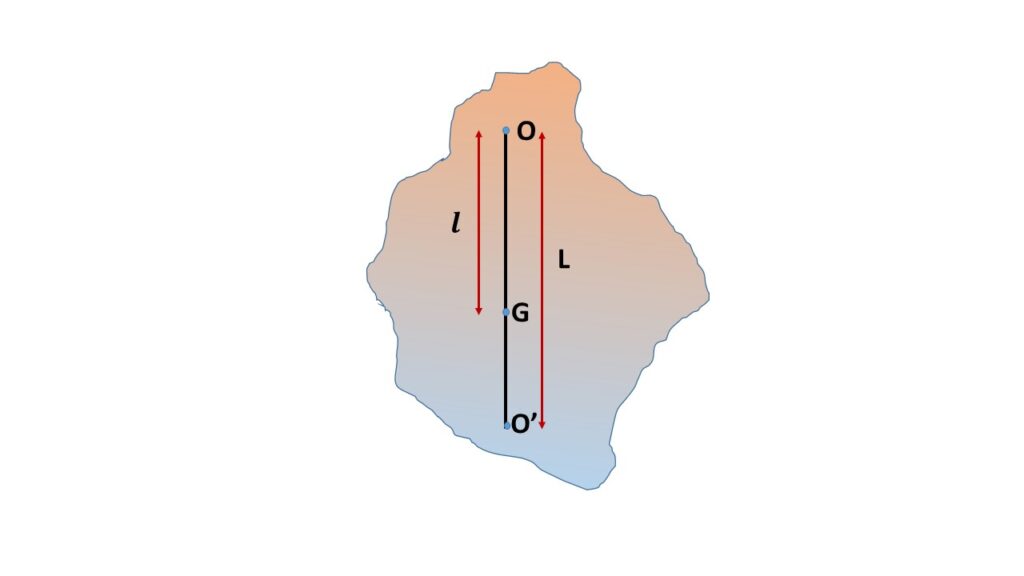
Let us consider a compound pendulum is suspended in a vertical plane from the horizontal axis through the point O and \( l \) be the distance of the centre of gravity G from the centre of suspension O.

So the time period oscillation of the compound pendulum is given by,

\( \displaystyle{T=2\pi\sqrt{\frac{K^2+l^2}{gl}}}\tag{1} \)
[ to know the derivation (CLICK HERE) ]

Where, K is the radius of gyration and \( g \) is the acceleration due to gravity.

or, \( \displaystyle{T^2=4{\pi}^2\frac{K^2+l^2}{lg}} \)

Differentiating both side with respect to \( l \), we get

\( \displaystyle{2T\frac{dT}{dl}=\frac{4{\pi}^2}{g}\left(1-\frac{K^2}{l^2}\right)} \)

or, \( \displaystyle{T\frac{dT}{dl}=\frac{2{\pi}^2}{g}\left(1-\frac{K^2}{l^2}\right)} \)

For \( T \) to be minimum \( \frac{dT}{dl}=0 \),

Therefore, \( 1-\frac{K^2}{l^2}=0 \)

or, \( K^2=l^2 \)

or, \( K=l \)

This is the condition for minimum time period of oscillation of the compound pendulum.

Minimum time period of oscillation of the compound pendulum:

Putting the value \( K=l \) is equation (1) we get

\( \displaystyle{T_{min}=2\pi\sqrt{\frac{K^2+K^2}{Kg}}} \)

or, \( \displaystyle{T_{min}=2\pi\sqrt{\frac{2K}{g}}} \)