(i) Moment of inertia of rectangular lamina about an axis parallel to its breadth and passing through its centre of mass:

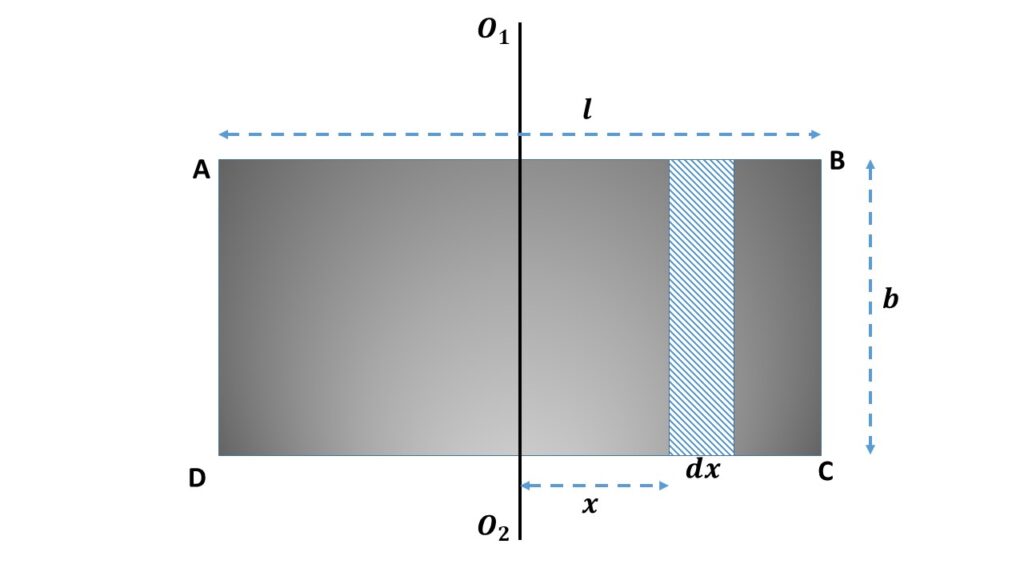
Let us consider a rectangular lamina ABCD of mass M, length \( l \) and breadth \( b \). So the surface area of this rectangular lamina is \( lb \) and mass density i.e., mass per unit area of this lamina is \( \left(\frac{M}{lb}\right) \). In order to calculate the moment of inertia of this rectangular lamina about the axis \( O_1O_2 \) passing through the centre of mass of this lamina and parallel to its breadth, let us consider a small elementary slice of length \( dx \) at a distance \( x \) from the axis \( O_1O_2 \). Now the area of this slice is \( b\ dx \) and the mass of this sliece is \( \left(\frac{M}{lb}\right)\cdot{b}\ dx \) = \( \left(\frac{M}{l}\right)dx \).
Now the moment of inertia of this slice about the axis \( O_1O_2 \) is \( \left(\frac{M}{l}\right)dx\times{x^2} \).

So the moment of inertia of this whole rectangular lamina about the axis of rotation \( O_1O_2 \) is

\( I_b=\displaystyle{\int_{-\frac{l}{2}}^{\frac{l}{2}}}\frac{M}{l}x^2\ dx \)

\( or,\ I_b=\frac{M}{l}\displaystyle{\int_{-\frac{l}{2}}^{\frac{l}{2}}}x^2\ dx \)

\( or,\ I_b=\frac{M}{l}\frac{1}{3}\left[x^3\right]_{-\frac{l}{2}}^{\frac{l}{2}} \)

\( or,\ I_b=\frac{M}{3l}\left[\frac{l^3}{8}+\frac{l^3}{8}\right] \)

\( or,\ \displaystyle{I_b=\frac{1}{12}Ml^2} \)

(ii) Moment of inertia of a rectangular lamina about an axis parallel to its length and passing through the centre of mass of the lamina, lies in the plane of the lamina:

Let us consider a rectangular lamina of mass M, length \( l \) and breadth \( b \). So the surface area of this rectangular lamina is \( lb \) and mass density i.e., mass per unit area of this lamina is \( \left(\frac{M}{lb}\right) \). In order to calculate the moment of inertia of this rectangular lamina about the axis \( O_3O_4 \) passing through the centre of mass of this lamina and parallel to its length, let us consider a small elementary slice of breadth \( dy \) and length \( l \) at a distance \( y \) from the axis \( O_3O_4 \). Now the area of this slice is \( l\ dy \) and the mass of this sliece is \( \left(\frac{M}{lb}\right)\cdot{l}\ dy \) = \( \left(\frac{M}{b}\right)dy \).

Now the moment of inertia of this slice about the axis \( O_3O_4 \) is \( \left(\frac{M}{b}\right)dy\times{y^2} \).

So the moment f inertia of this whole rectangular lamina about the axis \( O_3O_4 \) is

\( I_l=\displaystyle{\int_{-\frac{b}{2}}^{\frac{b}{2}}}\frac{M}{b}y^2\ dy \)

\( or,\ I_l=\frac{M}{b}\displaystyle{\int_{-\frac{b}{2}}^{\frac{b}{2}}}y^2\ dy \)

\( or,\ I_l=\frac{M}{b}\frac{1}{3}\left[y^3\right]_{-\frac{b}{2}}^{\frac{b}{2}} \)

\( or,\ I_l=\frac{M}{3b}\left[\frac{b^3}{8}+\frac{b^3}{8}\right] \)

\( or,\ \displaystyle{I_l=\frac{1}{12}Mb^2} \)

(iii) Moment of inetia of rectangular lamina about an axis passig through the centre of mass of the lamina and perpendicular to its plane:

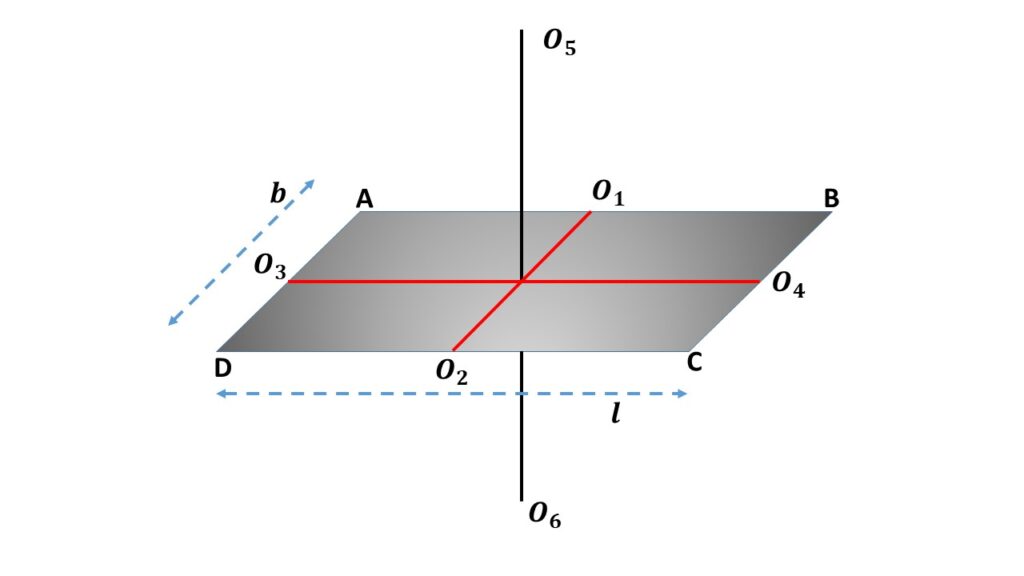
Now we want to calculate the moment of inertia of the rectangular lamina ABCD about an axis \( O_5O_6 \) passing through the centre of mass of the lamina and perpendicular to the plane of the lamina. So by using the theorem of perpendicular axes, we can write that the moment of inertia of the lamina ABCD about the axis \( O_5O_6 \) is given by,

\( I=I_b+I_l\\or,\ I=\frac{1}{12}Ml^2+\frac{1}{12}Mb^2 \)

\( or,\ \displaystyle{I=\frac{1}{12}M(l^2+b^2)} \)